题目内容
10.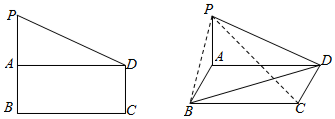 如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,PB=BC=2CD=2,点A是PB的中点,现沿AD将平面PAD折起,设∠PAB=θ:
如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,PB=BC=2CD=2,点A是PB的中点,现沿AD将平面PAD折起,设∠PAB=θ:(1)当θ为直角时,求异面直线PC与BD所成角的大小:
(2)当θ为多少度时,三棱锥P-ABD的体积为$\frac{\sqrt{2}}{6}$:
分析 (1)取PA的中点E,连结OE,BE,则∠BOP为PC,BD所成的角,由PA⊥AB,PA⊥AD可得PA⊥平面ABCD,利用勾股定理求出△OBE的三边长,使用余弦定理求出cos∠BOP;
(2)P到平面ABCD的距离为PAsinθ=sinθ,代入棱锥P-ABD的体积公式求出sinθ得出θ的值.
解答 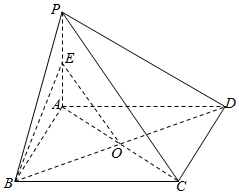 解:(1)∵AB∥CD,AB=CD,CD⊥BC,
解:(1)∵AB∥CD,AB=CD,CD⊥BC,
∴四边形ABCD是矩形,
连结AC交BD与O,则O是AC,BD的中点,
取PA的中点E,连结OE,BE,
则OE是△PAC的中位线,∴PC∥OE,OE=$\frac{1}{2}$PC.
∴∠BOE是异面直线PC,BD所成的角
∵PA⊥AB,PA⊥AD,AB∩AD=A,
∴PA⊥平面ABCD,
∴BE=$\sqrt{A{B}^{2}+A{E}^{2}}=\frac{\sqrt{5}}{2}$,OB=OA=$\frac{1}{2}$BD=$\frac{1}{2}$$\sqrt{A{B}^{2}+A{D}^{2}}=\frac{\sqrt{5}}{2}$.OE=$\sqrt{A{E}^{2}+O{A}^{2}}$=$\frac{\sqrt{6}}{2}$.
∴cos∠BOE=$\frac{O{B}^{2}+O{E}^{2}-B{E}^{2}}{2OB•OE}$=$\frac{\frac{5}{4}+\frac{6}{4}-\frac{5}{4}}{2×\frac{\sqrt{5}}{2}×\frac{\sqrt{6}}{2}}$=$\frac{\sqrt{30}}{10}$.
∴∠BOE=arccos$\frac{\sqrt{30}}{10}$.即异面直线PC与BD所成的角为arccos$\frac{\sqrt{30}}{10}$.
(2)P到平面ABCD的距离h=PAsinθ=sinθ.
S△ABD=$\frac{1}{2}AB×AD$=1,
∴VP-ABD=$\frac{1}{3}{S}_{△ABD}•h$=$\frac{1}{3}×1×sinθ$=$\frac{\sqrt{2}}{6}$.
∴sinθ=$\frac{\sqrt{2}}{2}$.
∴θ=$\frac{π}{4}$或$\frac{3π}{4}$.
点评 本题考查了异面直线所成角的计算,棱锥的体积计算,作出空间角是解题关键,也可使用向量法求出,属于中档题.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案| 日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
| 昼夜温差(.C) | 10 | 11 | 13 | 12 | 8 |
| 发芽数(颗) | 23 | 25 | 30 | 26 | 16 |
(2)请根据3月2日至3月4日的三组数据,求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(3)若由线性回归方程得到的估计数据与所需要检验的数据误差均不超过2颗,则认为得到的线性回归方程是可靠的,试用3月1日与3月5日的两组数据检验,问(2)中所得的线性回归方程是否可靠?
(参考公式:$\widehatb=\frac{{\sum_{i=1}^{i=n}{({{x_i}-\overline x})•({{y_i}-\overline y})}}}{{\sum_{i=1}^{i=n}{{{({{x_i}-\overline x})}^2}}}}$或$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-b$\overline{x}$)
| A. |  | B. |  | C. | 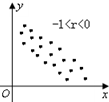 | D. | 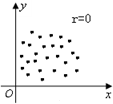 |
 如图所示,四边形ABCD为直角梯形,AB∥CD,AB⊥BC,△ABE为等边三角形,且平面ABCD⊥平面ABE,CD=BC=$\frac{1}{2}$AB=1,点P为CE中点.
如图所示,四边形ABCD为直角梯形,AB∥CD,AB⊥BC,△ABE为等边三角形,且平面ABCD⊥平面ABE,CD=BC=$\frac{1}{2}$AB=1,点P为CE中点.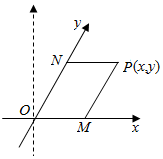 如图,将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后,构成一个斜坐标平面xOy.在此斜坐标平面xOy中,点P(x,y)的坐标定义如下:过点P作两坐标轴的平行线,分别交两轴于M,N两点,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.那么以原点O为圆心的单位圆在此斜坐标系下的方程为x2+y2+xy-1=0.
如图,将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后,构成一个斜坐标平面xOy.在此斜坐标平面xOy中,点P(x,y)的坐标定义如下:过点P作两坐标轴的平行线,分别交两轴于M,N两点,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.那么以原点O为圆心的单位圆在此斜坐标系下的方程为x2+y2+xy-1=0. 如图,在四棱锥S-ABCD中,侧棱SA⊥底面ABCD,且底面ABCD是边长为1的正方形,侧棱SA=4,AC与BD相交于点O.
如图,在四棱锥S-ABCD中,侧棱SA⊥底面ABCD,且底面ABCD是边长为1的正方形,侧棱SA=4,AC与BD相交于点O.