题目内容
对于各数互不相等的整数数组（i1，i2，i3，…，in）（n是不小于2的正整数），p，q∈{1，2，3，…，n}，当p＜q时有ip＞iq，则称ip，iq是该数组的一个“逆序”，一个数组中所有“逆序”的个数称为该数组的“逆序数”，则数组（5，2，4，3，1）中的逆序数等于 ．
考点：进行简单的合情推理
专题：计算题,推理和证明
分析：由于数组中包含的数字比较少，数组（5，2，4，3，1）中的逆序可以列举出共，8个
解答：
解：由题意知数组（5，2，4，3，1）中的逆序有5，2；5，4；5，3；5，1；2，1；4，1；3，1；4，3，
∴逆序数是，8
故答案为：8．
∴逆序数是，8
故答案为：8．
点评：本题是一个新定义问题，解题时需要读懂题意，才能做题，考查列举法，是一个非常新颖的问题．
练习册系列答案
相关题目
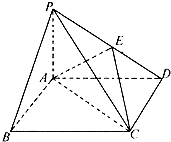四棱锥P-ABCD中，底面ABCD是边长为2的正方形，PB⊥BC，PD⊥CD，E是侧棱PD的中点．