题目内容
15.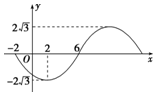 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示.(1)求此函数的解析式;
(2)求此函数的递增区间.
分析 (1)根据三角函数的图象求出A,ω,φ,即可确定函数的解析式;
(2)根据函数的表达式,利用正弦函数的性质即可求函数f(x)的单调递增区间;
解答 解:(1)由题图可知,其振幅为A=2$\sqrt{3}$,
由于$\frac{T}{2}$=6-(-2)=8,
所以周期为T=16,
所以ω=$\frac{2π}{T}$=$\frac{2π}{16}$=$\frac{π}{8}$,
此时解析式为y=2$\sqrt{3}$sin($\frac{π}{8}$x+φ).
因为点(2,-2$\sqrt{3}$)在函数y=2$\sqrt{3}$sin($\frac{π}{8}$x+φ)的图象上,
所以$\frac{π}{8}$×2+φ=2kπ-$\frac{π}{2}$(k∈Z),
所以φ=2kπ-$\frac{3π}{4}$(k∈Z).
又|φ|<π,所以φ=-$\frac{3π}{4}$.
故所求函数的解析式为y=2$\sqrt{3}$sin($\frac{π}{8}$x-$\frac{3π}{4}$).
(2)由2kπ-$\frac{π}{2}$≤$\frac{π}{8}$x-$\frac{3π}{4}$≤2kπ+$\frac{π}{2}$(k∈Z),得16k+2≤x≤16k+10(k∈Z),
所以函数y=2$\sqrt{3}$sin($\frac{π}{8}$x-$\frac{3π}{4}$)的递增区间是[16k+2,16k+10](k∈Z).
点评 本题主要考查三角函数解析式的求法,根据三角函数的图象是解决本题的关键,要求熟练掌握三角函数的图象和性质,属于基础题.

练习册系列答案
相关题目
20.若O为△ABC所在平面内任一点,且满足($\overrightarrow{OB}$-$\overrightarrow{OC}$)•($\overrightarrow{OB}$+$\overrightarrow{OC}$-2$\overrightarrow{OA}$)=0,则△ABC的形状为( )
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
10. 如图,一个正六角星薄片(其对称轴与水平面垂直)匀速地升长水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(x)的图象大致为( )
如图,一个正六角星薄片(其对称轴与水平面垂直)匀速地升长水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(x)的图象大致为( )
 如图,一个正六角星薄片(其对称轴与水平面垂直)匀速地升长水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(x)的图象大致为( )
如图,一个正六角星薄片(其对称轴与水平面垂直)匀速地升长水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(x)的图象大致为( )| A. | 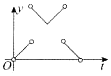 | B. | 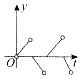 | C. | 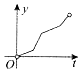 | D. |  |
20.已知直线m,n和平面α满足m⊥α,m⊥n,则n与α的位置关系为( )
| A. | n⊥α | B. | n?α | C. | n∥α或n?α | D. | 都有可能 |
5.若有99%的把握说事件A与事件B有关,那么具体算出的X2一定满足( )
| A. | X2>10.828 | B. | X2<10.828 | C. | X2>6.635 | D. | X2<6.635 |
 三棱锥P-ABC中,PC⊥平面ABC,F,G,H,分别是PC,AC,BC的中点,I是线段FG上任意一点,PC=AB=2BC=2.
三棱锥P-ABC中,PC⊥平面ABC,F,G,H,分别是PC,AC,BC的中点,I是线段FG上任意一点,PC=AB=2BC=2.