题目内容
如图,已知点P是三角形ABC外一点,且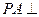 底面
底面
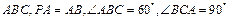 ,点
,点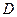 ,
,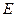 分别在棱
分别在棱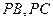 上,且
上,且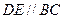 。 。
。 。
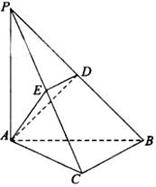
(1)求证: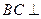 平面
平面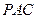 ;
;
(2)当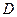 为
为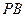 的中点时,求
的中点时,求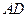 与平面
与平面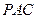 所成的角的大小;
所成的角的大小;
(3)是否存在点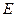 使得二面角
使得二面角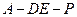 为直二面角?并说明理由.
为直二面角?并说明理由.
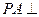 底面
底面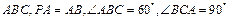 ,点
,点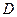 ,
,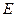 分别在棱
分别在棱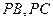 上,且
上,且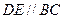 。 。
。 。 
(1)求证:
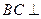 平面
平面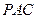 ;
;(2)当
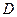 为
为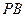 的中点时,求
的中点时,求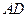 与平面
与平面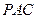 所成的角的大小;
所成的角的大小;(3)是否存在点
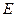 使得二面角
使得二面角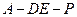 为直二面角?并说明理由.
为直二面角?并说明理由.(1)∵PA⊥底面ABC,∴PA⊥BC.
又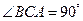 ,∴AC⊥BC.
,∴AC⊥BC.
∴BC⊥平面PAC.
(2)∵D为PB的中点,DE//BC,
∴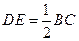 ,
,
又由(Ⅰ)知,BC⊥平面PAC,
∴DE⊥平面PAC,垂足为点E.
∴∠DAE是AD与平面PAC所成的角,
∵PA⊥底面ABC,∴PA⊥AB,又PA=AB,
∴△ABP为等腰直角三角形,∴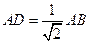 ,
,
∴在Rt△ABC中,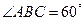 ,∴
,∴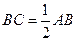 .
.
∴在Rt△ADE中,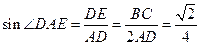 ,
,
∴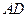 与平面
与平面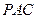 所成的角的大小
所成的角的大小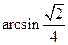 .
.
(3)∵AE//BC,又由(Ⅰ)知,BC⊥平面PAC,∴DE⊥平面PAC,
又∵AE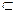 平面PAC,PE
平面PAC,PE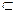 平面PAC,∴DE⊥AE,DE⊥PE,
平面PAC,∴DE⊥AE,DE⊥PE,
∴∠AEP为二面角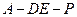 的平面角,
的平面角,
∵PA⊥底面ABC,∴PA⊥AC,∴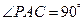 .
.
∴在棱PC上存在一点E,使得AE⊥PC,这时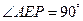 ,
,
故存在点E使得二面角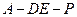 是直二面角.
是直二面角.
又
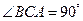 ,∴AC⊥BC.
,∴AC⊥BC.∴BC⊥平面PAC.
(2)∵D为PB的中点,DE//BC,
∴
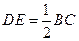 ,
,又由(Ⅰ)知,BC⊥平面PAC,
∴DE⊥平面PAC,垂足为点E.
∴∠DAE是AD与平面PAC所成的角,
∵PA⊥底面ABC,∴PA⊥AB,又PA=AB,
∴△ABP为等腰直角三角形,∴
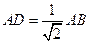 ,
,∴在Rt△ABC中,
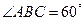 ,∴
,∴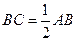 .
.∴在Rt△ADE中,
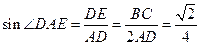 ,
,∴
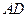 与平面
与平面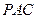 所成的角的大小
所成的角的大小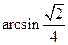 .
.(3)∵AE//BC,又由(Ⅰ)知,BC⊥平面PAC,∴DE⊥平面PAC,
又∵AE
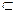 平面PAC,PE
平面PAC,PE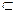 平面PAC,∴DE⊥AE,DE⊥PE,
平面PAC,∴DE⊥AE,DE⊥PE,∴∠AEP为二面角
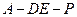 的平面角,
的平面角,∵PA⊥底面ABC,∴PA⊥AC,∴
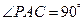 .
. ∴在棱PC上存在一点E,使得AE⊥PC,这时
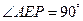 ,
,故存在点E使得二面角
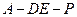 是直二面角.
是直二面角.略

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 侧棱与底面垂直,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
侧棱与底面垂直,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.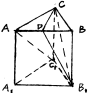
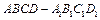 中,M、N、P、Q分别为AD、CD、
中,M、N、P、Q分别为AD、CD、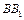 、
、 的中点.
的中点.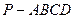 中,
中,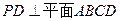 ,
,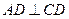 ,且DB平分
,且DB平分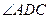 ,E为PC的中点,
,E为PC的中点,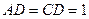 ,
,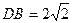 PD=3,(1)证明
PD=3,(1)证明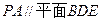 (2)证明
(2)证明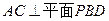
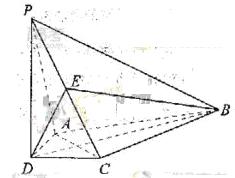
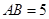 ,AA1=4,.点D是AB的中点.
,AA1=4,.点D是AB的中点.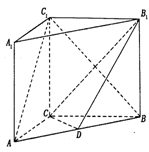
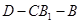 的平面角的正切值.
的平面角的正切值.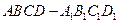 中,
中,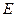 、
、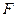 分别为
分别为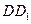 、
、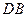 的中点. (1)求证: (1)、
的中点. (1)求证: (1)、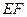 //平面
//平面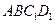 ;
;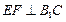 ;
;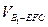 的体积.
的体积.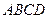 中,
中,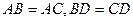 ,平面
,平面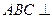 平面
平面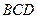 ,
,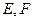 分别为棱
分别为棱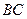 和
和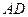 的中点。
的中点。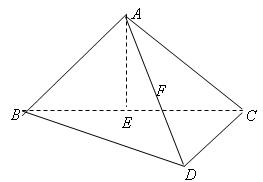
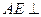 平面
平面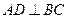 ;
;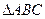 内的点
内的点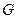 满足
满足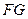 ∥平面
∥平面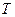 ,试描述点集
,试描述点集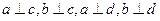 ,那么
,那么 面ABCD,
面ABCD,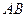 ∥
∥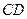 ,AD=CD=1,∠
,AD=CD=1,∠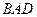 =120°,
=120°,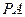 =
=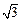 ,∠
,∠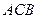 =90°,M是线段PD上的一点(不包括端点).
=90°,M是线段PD上的一点(不包括端点).