题目内容
20.根据下列条件求直线方程.(1)已知直线过点P(-2,2)且与两坐标轴所围成的三角形的面积为1;
(2)已知直线过两直线3x-2y+1=0和x+3y+4=0的交点,且垂直于直线x+3y+4=0.
分析 (1)引入两个截距,用截距式写出方程,代入点(-2,2)得到一个关于两个截距的方程,再用截距表示出与坐标轴所围成的三角形的面积,令其为1,得到另一个关于截距的方程,解这两个方程组成方程组,求出截距,写出方程即可.
(2)联立已知的两直线方程得到方程组,求出两直线的交点坐标,所求的直线过交点坐标,然后由两直线垂直时斜率的乘积等于-1,根据直线x+3y+4=0的斜率即可得到所求直线的斜率,利用点斜式求直线的方程即可.
解答 解:(1)设所求直线方程为$\frac{x}{a}$+$\frac{y}{b}$=1,由已知可得$\left\{\begin{array}{l}{\frac{-2}{a}+\frac{2}{b}=1}\\{\frac{1}{2}|a|•|b|=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=-2}\end{array}\right.$或$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$,
属于该直线方程为:2x+y+2=0或x+2y-2=0;
(2)联立直线方程 $\left\{\begin{array}{l}{3x-2y+1=0①}\\{x+3y+4=0②}\end{array}\right.$,
①+②×(-3)得:y=-1,把y=-1代入②,解得x=-1,
原方程组的解为:$\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$,
所以两直线的交点坐标为(-1,-1),
又因为直线x+3y+4=0的斜率为-$\frac{1}{3}$,所以所求直线的斜率为3,
则所求直线的方程为:y+1=3(x+1),即3x-y+2=0.
点评 考查用待定系数法求直线方程,本题先引入参数,表示出直线的方程,再根据题设的条件建立起参数的方程求参数,这是求直线方程时常用的一个思路.

| A. | $\frac{1}{3}$ | B. | -$\frac{1}{2}$ | C. | -1 | D. | -2 |
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
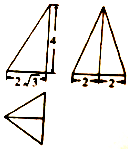 若一个几何体的三视图如图所示,则这个几何体的外接球的表面积为( )
若一个几何体的三视图如图所示,则这个几何体的外接球的表面积为( )| A. | 34π | B. | $\frac{80π}{3}$ | C. | $\frac{91}{3}π$ | D. | 114π |
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $-\frac{4}{5}$ |
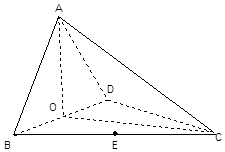 如图,四面体ABCD中,O、E分别是BD、BC的中点,底面BCD是正三角形,AC=BD=2,AB=AD=$\sqrt{2}$.
如图,四面体ABCD中,O、E分别是BD、BC的中点,底面BCD是正三角形,AC=BD=2,AB=AD=$\sqrt{2}$.