题目内容
如图,四棱锥G—ABCD中,ABCD是正方形,且边长为2a,面ABCD⊥面ABG,AG=BG。
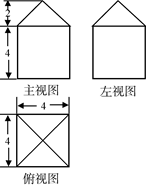
(1)画出四棱锥G—ABCD的三视图;
 |
 (2)在四棱锥G—ABCD中,过点B作平面
(2)在四棱锥G—ABCD中,过点B作平面AGC的垂线,若垂足H在CG上,
求证:面AGD⊥面BGC
(3)在(2)的条件下,求三棱锥D—ACG的体积
及其外接球的表面积。

(1)三视图(见右图)


(2)ABCD是正方形 ∴ BC⊥AB
∵面ABCD⊥面ABG ∴ BC⊥面ABG
∵AG 面ABG ∴ BC⊥AG
面ABG ∴ BC⊥AG
又 BH⊥面AGC ∴ BH⊥AG
∵ BC BH="B " ∴ AG⊥面AGD
BH="B " ∴ AG⊥面AGD
∴面AGD⊥面BGC
(3)由(2)知 AG⊥面BGC ∴AG⊥BG 又AG=BG
∴△ABG是等腰Rt△,取AB中点E,
连结GE,则GE⊥AB
∴ GE⊥面ABCD
∴
 又
又 ∴取AC中点M,则
∴取AC中点M,则  因此:
因此:
 即点M是三棱锥D—ACG的外接球的球心,
即点M是三棱锥D—ACG的外接球的球心,
半径为 ∴
∴ 


(2)ABCD是正方形 ∴ BC⊥AB
∵面ABCD⊥面ABG ∴ BC⊥面ABG
∵AG
 面ABG ∴ BC⊥AG
面ABG ∴ BC⊥AG又 BH⊥面AGC ∴ BH⊥AG
∵ BC
 BH="B " ∴ AG⊥面AGD
BH="B " ∴ AG⊥面AGD∴面AGD⊥面BGC
(3)由(2)知 AG⊥面BGC ∴AG⊥BG 又AG=BG
∴△ABG是等腰Rt△,取AB中点E,
连结GE,则GE⊥AB
∴ GE⊥面ABCD
∴

 又
又 ∴取AC中点M,则
∴取AC中点M,则  因此:
因此: 即点M是三棱锥D—ACG的外接球的球心,
即点M是三棱锥D—ACG的外接球的球心,半径为
 ∴
∴ 

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
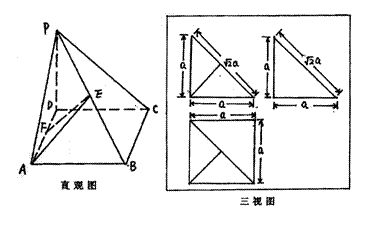
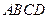 中,
中,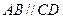 ,
,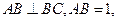
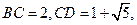 过
过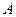 作
作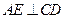 ,垂足为
,垂足为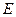 ,
,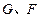 分别为
分别为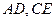 的中点,现将
的中点,现将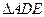 沿
沿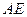 折叠使二面角
折叠使二面角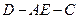 的平面角的正切值为
的平面角的正切值为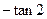 .
.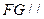 平面
平面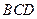 ;
;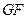 与
与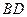 所成的角的余弦值;
所成的角的余弦值;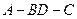 的大小.
的大小.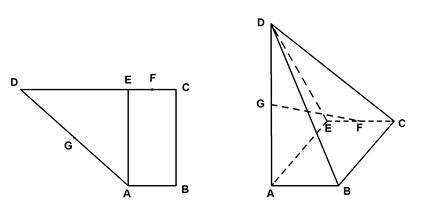
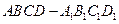 中,
中,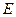 、
、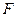 分别是棱
分别是棱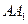 、
、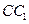 的中点.
的中点.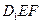 与平面
与平面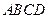 的交线.
的交线.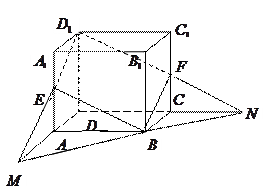
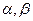 为互不重合的平面,
为互不重合的平面,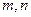 为互不重合的直线,给出下列四个命题:]
为互不重合的直线,给出下列四个命题:]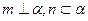 则
则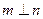 ;
;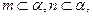
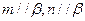 ,则
,则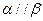 ;
;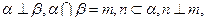 则
则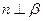
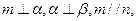 则
则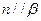
 8.
8. cm
cm
 cm
cm