题目内容
已知直角梯形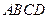 中,
中,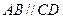 ,
,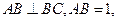
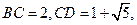 过
过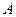 作
作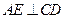 ,垂足为
,垂足为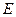 ,
,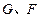 分别为
分别为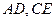 的中点,现将
的中点,现将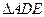 沿
沿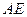 折叠使二面角
折叠使二面角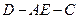 的平面角的正切值为
的平面角的正切值为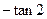 .
.
(1)求证: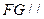 平面
平面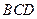 ;
;
(2)求异面直线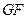 与
与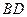 所成的角的余弦值;
所成的角的余弦值;
(3)求二面角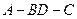 的大小.
的大小.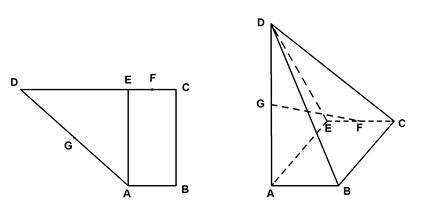
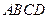 中,
中,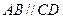 ,
,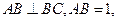
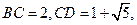 过
过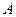 作
作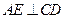 ,垂足为
,垂足为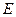 ,
,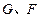 分别为
分别为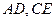 的中点,现将
的中点,现将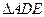 沿
沿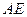 折叠使二面角
折叠使二面角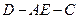 的平面角的正切值为
的平面角的正切值为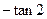 .
.(1)求证:
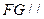 平面
平面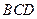 ;
;(2)求异面直线
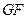 与
与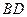 所成的角的余弦值;
所成的角的余弦值;(3)求二面角
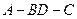 的大小.
的大小.
(1)见解析(2) (3)
(3)
 (3)
(3)
(1)取 中点
中点 ,连接
,连接 ,
, ,又
,又 为
为 中点
中点
 ,
, 平面
平面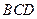 ,
, 平面
平面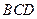 ,
, , 同理可证
, 同理可证  ,
, 平面
平面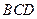 ,
, 平面
平面 平面
平面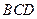 ,
,  平面
平面
 平面
平面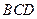 .
.
(2)延长 ,过
,过 作
作 垂直直线
垂直直线 于
于 ,易证
,易证 平面
平面 ,
, ,
, ,二面角
,二面角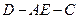 的平面角的正切值为
的平面角的正切值为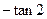 ,∴
,∴
∵ ,∴
,∴ ,
, ,过点
,过点 做
做 ,以
,以 为原点,以射线
为原点,以射线 分别为
分别为 的正方向建立直角坐标系
的正方向建立直角坐标系 (如图)
(如图)
则 ,
, ,
, ,
, ,
, ,
, ,
, ,
, .
.
 ,
,
 ,
,
∴异面直线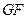 与
与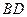 所成的角余弦值为
所成的角余弦值为 .
.

(3)取 中点
中点 ,易证
,易证 平面
平面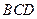 ,所以面
,所以面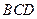 一个法向量为
一个法向量为
 ,
, ,设平面
,设平面 的法向量为
的法向量为
则 ,
,
取 得
得 得平面
得平面 的一个法向量为
的一个法向量为 ∴
∴
∴二面角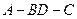 的大小为.
的大小为.
 中点
中点 ,连接
,连接 ,
, ,又
,又 为
为 中点
中点 ,
, 平面
平面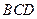 ,
, 平面
平面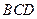 ,
, , 同理可证
, 同理可证  ,
, 平面
平面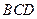 ,
, 平面
平面 平面
平面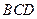 ,
,  平面
平面
 平面
平面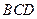 .
.(2)延长
 ,过
,过 作
作 垂直直线
垂直直线 于
于 ,易证
,易证 平面
平面 ,
, ,
, ,二面角
,二面角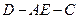 的平面角的正切值为
的平面角的正切值为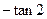 ,∴
,∴
∵
 ,∴
,∴ ,
, ,过点
,过点 做
做 ,以
,以 为原点,以射线
为原点,以射线 分别为
分别为 的正方向建立直角坐标系
的正方向建立直角坐标系 (如图)
(如图)则
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, .
. ,
,
 ,
, ∴异面直线
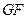 与
与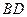 所成的角余弦值为
所成的角余弦值为 .
.
(3)取
 中点
中点 ,易证
,易证 平面
平面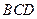 ,所以面
,所以面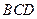 一个法向量为
一个法向量为
 ,
, ,设平面
,设平面 的法向量为
的法向量为
则
 ,
,取
 得
得 得平面
得平面 的一个法向量为
的一个法向量为 ∴
∴
∴二面角
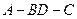 的大小为.
的大小为.
练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
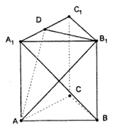
 如图,四棱柱ABCD—A1B1C1D1的底面边长和侧棱长都等于2,平面A1ACC1⊥平面ABCD,∠ABC=∠A1AC=60°,点O为底面对角线AC与BD的交点.
如图,四棱柱ABCD—A1B1C1D1的底面边长和侧棱长都等于2,平面A1ACC1⊥平面ABCD,∠ABC=∠A1AC=60°,点O为底面对角线AC与BD的交点.

 的三视图如图所 示,其中
的三视图如图所 示,其中 分别是
分别是 五点在直立、侧立、水平三个投影面内的投影,且在主视图中,四边形
五点在直立、侧立、水平三个投影面内的投影,且在主视图中,四边形 为正方形且
为正方形且 ;在左视图中
;在左视图中 俯视图中
俯视图中 ,
, 作平面
作平面 的垂线,若垂足H在直线
的垂线,若垂足H在直线 上,求证:平面
上,求证:平面 ⊥平面
⊥平面 ;
; 的体积及其外接球的表面积.
的体积及其外接球的表面积.
 (2)在四棱锥G—ABCD中,过点B作平面
(2)在四棱锥G—ABCD中,过点B作平面
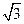
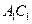
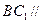 平面
平面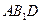
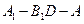 的大小
的大小