题目内容
如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.求证:PA∥平面EDB. 

连结AC,AC交BD于O,连结EO.
因为底面ABCD是正方形,

所以点O是AC的中点.
在△PAC中,EO是中位线,
所以PA∥EO.
而 平面EDB,且
平面EDB,且 平面EDB,
平面EDB,
所以PA∥平面EDB.
因为底面ABCD是正方形,

所以点O是AC的中点.
在△PAC中,EO是中位线,
所以PA∥EO.
而
 平面EDB,且
平面EDB,且 平面EDB,
平面EDB,所以PA∥平面EDB.
空间直线和平面

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 (2)在四棱锥G—ABCD中,过点B作平面
(2)在四棱锥G—ABCD中,过点B作平面 ②
② m∥n;③
m∥n;③ m⊥n;④
m⊥n;④ n⊥α.
n⊥α.
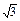 ,EF=2.
,EF=2.