题目内容
19.已知数列{an}的各项规律如下:a1=1+1×2,a2=1+2×3,a3=1+3×4,a4=1+4×5…若bn=$\frac{{a}_{n}-1}{n}$,则数列{bn}的前n项和为$\frac{1}{2}$(n2+3n).
分析 由条件可得an=1+n(n+1),求得bn=n+1,运用等差数列的求和公式,计算即可得到所求和.
解答 解:由a1=1+1×2,a2=1+2×3,a3=1+3×4,a4=1+4×5,…
可得an=1+n(n+1),
bn=$\frac{{a}_{n}-1}{n}$=$\frac{1+n(n+1)-1}{n}$=n+1,
则数列{bn}的前n项和为$\frac{1}{2}$n(2+n+1)=$\frac{1}{2}$(n2+3n).
故答案为:$\frac{1}{2}$(n2+3n).
点评 本题考查数列的通项和求和,注意运用归纳法和等差数列的求和公式,考查观察和归纳能力,属于基础题.

练习册系列答案
相关题目
9.已知点A的坐标为A(1,1,0),向量$\frac{1}{2}$$\overrightarrow{AB}$=(4,0,2),则点B的坐标为( )
| A. | (7,-1,4) | B. | (9,1,4) | C. | (3,1,1) | D. | (1,-1,1) |
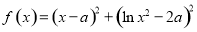 ,其中
,其中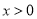 ,
,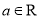 ,存在
,存在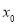 使得
使得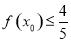 成立,则实数
成立,则实数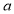 的值为( )
的值为( ) B.
B.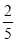 C.
C.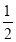 D.
D.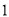
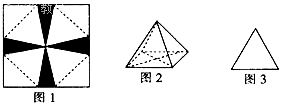 将一张边长为6cm的纸片按如图l所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥(底面是正方形,顶点在底面的射影为正方形的中心)模型,如图2放置.若正四棱锥的正视图是正三角形(如图3),则正四棱锥的体积是$\frac{8\sqrt{6}}{3}$.
将一张边长为6cm的纸片按如图l所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥(底面是正方形,顶点在底面的射影为正方形的中心)模型,如图2放置.若正四棱锥的正视图是正三角形(如图3),则正四棱锥的体积是$\frac{8\sqrt{6}}{3}$.