题目内容
5.空间几何体的三视图如图所示,则该几何体的体积为( )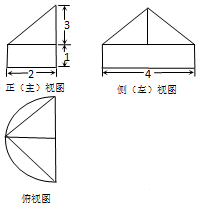
| A. | 4+2π | B. | 12+2π | C. | 4+4π | D. | 12+4π |
分析 由三视图可得,直观图是半圆柱与三棱锥的组合体,利用体积公式,即可求出体积.
解答 解:由三视图可得,直观图是半圆柱与三棱锥的组合体,体积为$\frac{1}{2}•π•{2}^{2}•1+\frac{1}{3}×\frac{1}{2}×4×2×3$=4+2π,
故选A.
点评 本题考查了由三视图求几何体的体积,解题的关键是判断几何体的形状及数据所对应的几何量.

练习册系列答案
相关题目
13.若实数x,y满足$\left\{\begin{array}{l}{x-y+1>0}\\{2x-y<0}\end{array}\right.$,则点P(x,y)不可能落在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.已知直线y=$\frac{2\sqrt{5}}{5}$x与双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)交于A、B两点,若在双曲线上存在点P,使得|PA|=|PB|=$\frac{\sqrt{3}}{2}$|AB|,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{5}$ |
 的值是( )
的值是( ) B.
B. C.
C. D.
D.
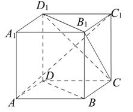
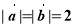 ,向量
,向量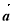 与
与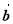 的夹角为
的夹角为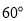 ,则
,则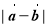 等于( )
等于( )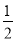 B.
B.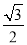 C.2 D.4
C.2 D.4