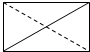
题目内容
11.双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的两个焦点分别为F1、F2,以F1F2为边作正△MF1F2,若双曲线恰好平分该三角形的另两边,则双曲线的离心率为( )| A. | $\sqrt{2}$+1 | B. | $\sqrt{3}$+1 | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
分析 根据双曲线的对称性可推断出三角形的顶点在y轴,根据正三角形的性质求得顶点的坐标,进而求得正三角形的边与双曲线的交点,代入双曲线方程与b2=c2-a2联立整理求得e.
解答 解:双曲线恰好平分正三角形的另两边,
顶点就在Y轴上坐标是(0,$\sqrt{3}$c)或(0,-$\sqrt{3}$c)
那么正三角形的边与双曲线的交点就是边的中点($\frac{1}{2}c$,$\frac{\sqrt{3}}{2}$c)
在双曲线上代入方程$\frac{{c}^{2}}{4{a}^{2}}-\frac{3{c}^{2}}{4{b}^{2}}$=1
联立b2=c2-a2求得e4-8e2+4=0
求得e=$\sqrt{3}$+1
故选:B.
点评 本题主要考查了双曲线的简单性质.考查了学生对双曲线基础知识的综合把握.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
13.直线kx-y+1-3k=0,当k变化是,所有直线恒过定点( )
| A. | (0,0) | B. | (3,1) | C. | (1,3) | D. | (-1,-3) |
14.若函数f(x)=e-x+ax(a∈R)在区间(1,+∞)上为增函数,则a的取值范围是( )
| A. | (0,+∞) | B. | [0,+∞) | C. | ($\frac{1}{e}$,+∞) | D. | [$\frac{1}{e}$,+∞) |
16.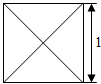 已知某几何体的俯视图是如图所示的边长为1的正方形,主视图与左视图是边长为1的正三角形,则其全面积是( )
已知某几何体的俯视图是如图所示的边长为1的正方形,主视图与左视图是边长为1的正三角形,则其全面积是( )
 已知某几何体的俯视图是如图所示的边长为1的正方形,主视图与左视图是边长为1的正三角形,则其全面积是( )
已知某几何体的俯视图是如图所示的边长为1的正方形,主视图与左视图是边长为1的正三角形,则其全面积是( )| A. | 2 | B. | 3 | C. | $1+\sqrt{3}$ | D. | $\sqrt{3}$ |
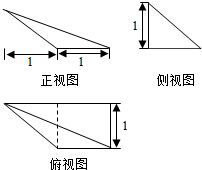
20.某几何体的三视图如图所示,则该几何体的体积是( )
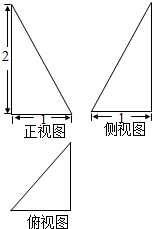

| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{3}$ |