题目内容
3．一个长方体的四个顶点构成一个四面体EFHG，在这个长方体中把四面体EFHG截出如图所示，则四面体EFHG的侧视图是（ ）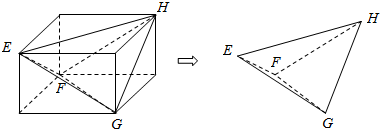
| A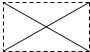． |  | B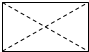． |  | C． |  | D． |  |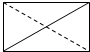
分析 根据已知中的四面体，分析轮廓形状及虚线实线情况，及两条对角线的虚线实线情况，可得答案．
解答 解：四面体EFHG的侧视图是从左向右方向上的投影，
此时投影的外轮廓是一个矩形，为实线；
对角线EF从右上角到左下角，为实线；
对角线HG从左上角到右下角，为虚线；
故选：D
点评 本题考查的知识点是空间几何体的三视图，解正确理解三视图的定义和画法，是解答的关键．
练习册系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
11．双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）的两个焦点分别为F1、F2，以F1F2为边作正△MF1F2，若双曲线恰好平分该三角形的另两边，则双曲线的离心率为（ ）
| A． | $\sqrt{2}$+1 | B． | $\sqrt{3}$+1 | C． | $\sqrt{5}$ | D． | $\sqrt{3}$ |
18．圆心在抛物线y2=2x（y＞0）上，并且与抛物线的准线及x轴都相切的方程是（ ）
| A． | x2+y2-x-2y-$\frac{1}{4}$=0， | B． | x2+y2+x-2y+1=0， | ||
| C． | x2+y2-x+1=0， | D． | x2+y2-x-2y+$\frac{1}{4}$=0， |
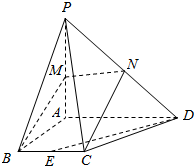在四棱锥P-ABCD中，底面ABCD为直角梯形，AB、AD、AP互相垂直，AD=2BC，过BC的平面分别交PA、PD于M、N两点（M不与A重合）．
15．正视图和俯视图为全等矩形的几何体不可能是（ ）
| A． | 四棱锥 | B． | 圆柱 | C． | 长方体 | D． | 三棱柱 |
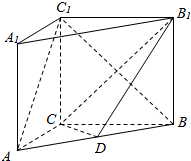如图，在直三棱柱（侧棱垂直底面的棱柱）ABC-A1B1C1中，∠ACB=90°，AC=3，BC=4，AA1=4，点D是AB的中点．