题目内容
9.点P在双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右支上,其左、右焦点分别为F1,F2,直线PF1与以坐标原点O为圆心,a为半径的圆相切于点A,线段PF1的垂直平分线恰好过点F2,则$\frac{{S}_{△O{F}_{1}A}}{{S}_{△P{F}_{1}{F}_{2}}}$的值为( )| A. | $\frac{1}{7}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{8}$ |
分析 由题意,线段PF1的垂直平分线恰过点F2,垂直为D,则yA=$\frac{1}{4}$yp,根据三角形的面积公式计算即可.
解答 解:由题意,线段PF1的垂直平分线恰过点F2,垂直为D,则yD=2yA=$\frac{1}{2}$yp,yA=$\frac{1}{4}$yp,
∴$\frac{{S}_{△O{F}_{1}A}}{{S}_{△P{F}_{1}{F}_{2}}}$=$\frac{\frac{1}{2}c•{y}_{A}}{\frac{1}{2}•2c•{y}_{D}}$=$\frac{1}{8}$,
故选:D.
点评 本题考查了双曲线的简单性质和三角形的面积公式,属于基础题.

练习册系列答案
相关题目
19.在(x2-4)(x+$\frac{1}{x}$)9的展开式中x5的系数为( )
| A. | 36 | B. | -144 | C. | 60 | D. | -60 |
17.祖暅原理:“幂势既同,则积不容异”.它是中国古代一个设计几何体体积的问题.意思是如果两个等高的几何体在同高处处截得两几何体的截面面积恒等,那么这两个几何体的体积相等.设A,B为两个等高的几何体,p:A,B的体积不相等,q:A,B在同高处的截面面积不恒相等,根据祖暅原理可知,p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.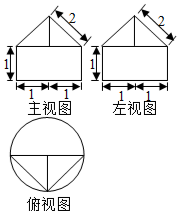 一个几何体的三视图如图所示,则该几何体的体积为( )
一个几何体的三视图如图所示,则该几何体的体积为( )
 一个几何体的三视图如图所示,则该几何体的体积为( )
一个几何体的三视图如图所示,则该几何体的体积为( )| A. | 2π+$\frac{\sqrt{3}}{3}$ | B. | π+$\frac{\sqrt{3}}{3}$ | C. | 2π+$\frac{\sqrt{3}}{3}$ | D. | π+$\sqrt{3}$ |
14.在高中学习过程中,同学们经常这样说:“数学物理不分家,如果物理成绩好,那么学习数学就没什么问题.”某班针对“高中生物理学习对数学学习的影响”进行研究,得到了苏俄生的物理成绩与数学成绩具有线性相关关系的结论.现从该班随机抽取5名学生在一次考试中的数学和物理成绩,如表:
(1)求数学成绩y对物理成绩x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$($\widehat{b}$精确到0.1).若某位学生的物理成绩为80分,预测他的数学成绩;
(2)要从抽取的这五位学生中随机选出2位参加一项知识竞赛,求选中的学生的数学成绩至少有一位高于120分的概率.(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
(参考数据:902+852+742+682+632=29394,90××125+74×110+68×95+63×90=42595)
| 成绩 编号 | 1 | 2 | 3 | 4 | 5 |
| 物理(x) | 90 | 85 | 74 | 68 | 63 |
| 数学(y) | 130 | 125 | 110 | 95 | 90 |
(2)要从抽取的这五位学生中随机选出2位参加一项知识竞赛,求选中的学生的数学成绩至少有一位高于120分的概率.(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
(参考数据:902+852+742+682+632=29394,90××125+74×110+68×95+63×90=42595)
1.设集合M={x|x=2n,n∈Z},N={x|x=2n+1,n∈Z},P={x|x=4n,n∈Z},则( )
| A. | M=P | B. | P≠M | C. | N∩P≠∅ | D. | M∩N≠∅ |
18.设a,b均为实数,则“a>|b|”是“a3>b3”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |