题目内容
11．化简：$\sqrt{1-sin2}$=（ ）| A． | sin1°-cos1° | B． | cos1°-sin1° | C． | sin1-cos1 | D． | cos1-sin1 |
分析 由于$\frac{π}{4}＜1＜\frac{π}{2}$，可得sin1＞cos1．由$\sqrt{1-sin2}$=|sin1-cos1|，即可得出．
解答 解：∵$\frac{π}{4}＜1＜\frac{π}{2}$，
∴sin1＞cos1．
∴$\sqrt{1-sin2}$=$\sqrt{（sin1-cos1）^{2}}$=sin1-cos1，
故选：C．
点评 本题考查了三角函数的单调性、乘法公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
2．全集U={（x，y）|x∈R，y∈R}，集合S⊆U，若S中的点在直角坐标平面内形成的图形关于原点、坐标轴、直线y=x均对称，且（2，3）∈S，则S中元素个数至少有（ ）
| A． | 4个 | B． | 6个 | C． | 8个 | D． | 10个 |
6．设β=-123°-3×180°，则角β是（ ）
| A． | 第一象限角 | B． | 第二象限角 | C． | 第三象限角 | D． | 第四象限角 |
16．已知数列{an}的首项为15，满足$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{{a}_{n}+2n}{{a}_{n+1}-2n}$，an+an+1≠0，且$\frac{{a}_{n}}{n}$＞λ2-3λ恒成立，则实数λ的取值范围为（ ）
| A． | -2＜λ＜3 | B． | λ≤-2或λ≥3 | C． | -$\frac{3}{2}$＜λ＜$\frac{9}{2}$ | D． | λ≤-$\frac{3}{2}$或λ≥$\frac{9}{2}$ |
13．
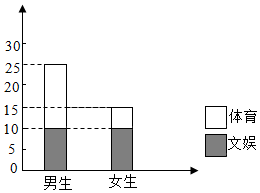对某班学生是爱好体育还是爱好文娱进行调查，根据调查得到的数据，所绘制的二维条形图如图．
（1）根据图中数据，制作2×2列联表；
（2）若要采用分层抽样的方法从男生中共抽取5名候选人，再从5人中选两人分别做文体活动协调人，求选出的两人恰好是一人更爱好文娱，另一人更爱好体育的学生的概率；
（3）是否可以认为性别与是否爱好体育有关系？
参考数据：
对某班学生是爱好体育还是爱好文娱进行调查，根据调查得到的数据，所绘制的二维条形图如图．（1）根据图中数据，制作2×2列联表；
（2）若要采用分层抽样的方法从男生中共抽取5名候选人，再从5人中选两人分别做文体活动协调人，求选出的两人恰好是一人更爱好文娱，另一人更爱好体育的学生的概率；
（3）是否可以认为性别与是否爱好体育有关系？
参考数据：
| P（K2≥k） | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |