题目内容
已知函数f(x)=2cosxsin(x+ )-
)- sin2x+sinxcosx
sin2x+sinxcosx
(1)求函数f(x)的最小正周期;
(2)求f(x)的最小值及取得最小值时相应的x的值;
(3)若当x∈[ ,
, ]时,f(x)的反函数为f-1(x),求f--1(1)的值。
]时,f(x)的反函数为f-1(x),求f--1(1)的值。
 )-
)- sin2x+sinxcosx
sin2x+sinxcosx(1)求函数f(x)的最小正周期;
(2)求f(x)的最小值及取得最小值时相应的x的值;
(3)若当x∈[
 ,
, ]时,f(x)的反函数为f-1(x),求f--1(1)的值。
]时,f(x)的反函数为f-1(x),求f--1(1)的值。(1) f(x)的最小正周期T=π, (2) x=kπ-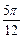 (k∈Z)时,f(x)取得最小值-2,(3) f--1(1)=
(k∈Z)时,f(x)取得最小值-2,(3) f--1(1)=
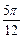 (k∈Z)时,f(x)取得最小值-2,(3) f--1(1)=
(k∈Z)时,f(x)取得最小值-2,(3) f--1(1)=
(1)f(x)=2cosxsin(x+ )-
)- sin2x+sinxcosx
sin2x+sinxcosx
=2cosx(sinxcos +cosxsin
+cosxsin )-
)- sin2x+sinxcosx
sin2x+sinxcosx
=2sinxcosx+ cos2x=2sin(2x+
cos2x=2sin(2x+ )
)
∴f(x)的最小正周期T=π
(2)当2x+ =2kπ-
=2kπ-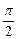 ,即x=kπ-
,即x=kπ- (k∈Z)时,f(x)取得最小值-2.
(k∈Z)时,f(x)取得最小值-2.
(3)令2sin(2x+ )=1,又x∈[
)=1,又x∈[ ],
],
∴2x+ ∈[
∈[ ,
, ],∴2x+
],∴2x+ =
=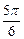 ,
,
则x= ,故f--1(1)=
,故f--1(1)= .
.
 )-
)- sin2x+sinxcosx
sin2x+sinxcosx=2cosx(sinxcos
 +cosxsin
+cosxsin )-
)- sin2x+sinxcosx
sin2x+sinxcosx=2sinxcosx+
 cos2x=2sin(2x+
cos2x=2sin(2x+ )
)∴f(x)的最小正周期T=π
(2)当2x+
 =2kπ-
=2kπ-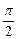 ,即x=kπ-
,即x=kπ- (k∈Z)时,f(x)取得最小值-2.
(k∈Z)时,f(x)取得最小值-2.(3)令2sin(2x+
 )=1,又x∈[
)=1,又x∈[ ],
],∴2x+
 ∈[
∈[ ,
, ],∴2x+
],∴2x+ =
=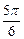 ,
,则x=
 ,故f--1(1)=
,故f--1(1)= .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
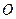 为坐标原点,向量
为坐标原点,向量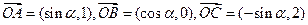 ,点
,点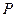 是直线
是直线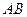 上的一点,且点
上的一点,且点 分有向线段
分有向线段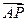 的比为
的比为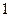 .
.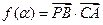 ,
,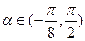 ,讨论函数
,讨论函数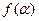 的单调性,并求其值域;
的单调性,并求其值域;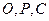 三点共线,求
三点共线,求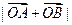 的值.
的值.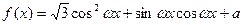 (其中
(其中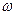 >0,
>0,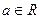 ),且
),且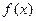 的图象在y轴右侧的第一个高点的横坐标为
的图象在y轴右侧的第一个高点的横坐标为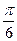 .(1)求
.(1)求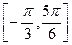 上的最小值为
上的最小值为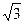 ,求a的值.
,求a的值.
 (米)是时间
(米)是时间 (
( ,单位:时)的函数,记作
,单位:时)的函数,记作 , 下面是某日水深的数据:
, 下面是某日水深的数据: 的图象,根据以上的数据,可得函数
的图象,根据以上的数据,可得函数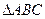 中,设内角A、B、C的对边分别为a、b、c,
中,设内角A、B、C的对边分别为a、b、c,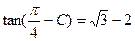
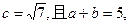 求
求 =__________.
=__________.