题目内容
20．若集合$A=\{x|\frac{2x-3}{x+1}≤1\}，B=\{x||x|≤3\}$，则A∩B=（ ）| A． | （-1，3] | B． | [-1，3] | C． | [-3，3] | D． | [-3，-1） |
分析 分别解关于A、B的不等式，求出交集即可．
解答 解：解不等式$\frac{2x-3}{x+1}$≤1，解得：-1＜x≤4，
∴A=（-1，4]，
集合B={x|-3≤x≤3}，
则A∩B=（-1，3]，
故选：A．
点评 本题考查了集合的运算，考查解不等式问题，是一道基础题．
练习册系列答案
相关题目
15．已知函数$f（x）=\left\{\begin{array}{l}sin（\frac{π}{2}x）-1，x＜0\\{log_a}x（a＞0，a≠1），x＞0\end{array}\right.$的图象上关于y轴对称的点至少有5对，则实数的取值范围是（ ）
| A． | .$（0，\frac{{\sqrt{5}}}{5}）$ | B． | $（\frac{{\sqrt{5}}}{5}，1）$ | C． | $（0，\frac{1}{3}）$ | D． | $（\frac{1}{3}，1）$ |
5．已知函数$f（x）=\left\{\begin{array}{l}{x^2}+x+1，x≥0\\ 2x+1，x＜0\end{array}\right.$，若f（sinα-sinβ+sin15°-1）=-1，f（cosα-cosβ+cos15°+1）=3，则cos（α-β）=（ ）
| A． | -2 | B． | 2 | C． | $-\frac{1}{2}$ | D． | $\frac{1}{2}$ |
12．已知函数y=f（|x|）在[-1，1]上的图象如图甲所示，则y=f（x）在[-1，1]上的图象可能是图乙中的（ ）
| A． | ①② | B． | ①③ | C． | ②③ | D． | ②④ |
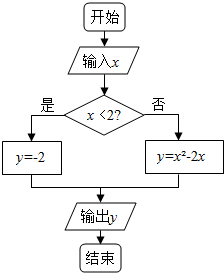据如图所示的程序框图，说明该流程图解决什么问题，写出相应的算法．并回答下列问题