题目内容
(14分)已知数列![]() 的前
的前![]() 项和
项和![]() 和通项
和通项![]() 满足
满足![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ) 求证:![]() ;
;
(Ⅲ)设函数![]() ,
,![]() ,求
,求![]() .
.
解析:(Ⅰ)当![]() 时
时
![]() ,
,![]()
∴![]() ,---------------------------------------------------------------------------3分
,---------------------------------------------------------------------------3分
由![]() 得
得![]()
∴数列![]() 是首项
是首项![]() 、公比为
、公比为![]() 的等比数列,∴
的等比数列,∴![]() ------5分
------5分
(Ⅱ)证法1: 由![]() 得
得![]()
![]() ---------------------------------7分
---------------------------------7分
![]() ,∴
,∴![]()
∴![]() ---------------------------------------------------------9分
---------------------------------------------------------9分
〔证法2:由(Ⅰ)知![]() ,
,
∴ 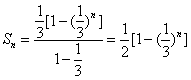 --------------------------------7分
--------------------------------7分
![]() ,∴
,∴![]() ---------------------------------8分
---------------------------------8分
即![]() -------------------------------------------------9分
-------------------------------------------------9分
(Ⅲ) ![]()
![]() =
=![]() -----------10分
-----------10分
=![]() -------------------12分
-------------------12分
∵![]()
∴![]()
![]()
![]() =
=![]() --------14分
--------14分

练习册系列答案
相关题目
 的前
的前 项和
项和 和通项
和通项 满足
满足 (
( 是常数且
是常数且 )。
)。 时,试证明
时,试证明 ;
; (Ⅲ)设函数
(Ⅲ)设函数 ,
, ,是否存在正整数
,是否存在正整数 ,使
,使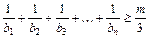 对
对 都成立?若存在,求出
都成立?若存在,求出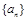 的前
的前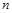 项和
项和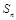 和通项
和通项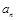 满足
满足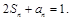 数列
数列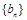 中,
中,
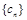 满足
满足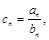 是否存在正整数
是否存在正整数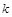 ,使得
,使得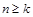 时
时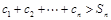 恒成立?若存在,求
恒成立?若存在,求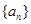 的前
的前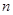 项和
项和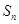 和通项
和通项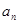 满足
满足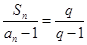 (
(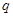 是常数且
是常数且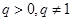 )。
)。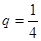 时,试证明
时,试证明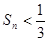 ;
;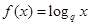 ,
, ,是否存在正整数
,是否存在正整数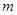 ,使
,使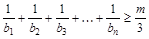 对
对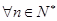 都成立?若存在,求出
都成立?若存在,求出