题目内容
已知数列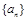 的前
的前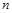 项和
项和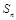 和通项
和通项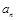 满足
满足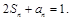 数列
数列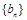 中,
中,

(1)求数列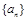 ,
,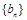 的通项公式;
的通项公式;
(2)数列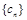 满足
满足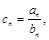 是否存在正整数
是否存在正整数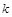 ,使得
,使得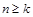 时
时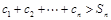 恒成立?若存在,求
恒成立?若存在,求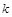 的最小值;若不存在,试说明理由.
的最小值;若不存在,试说明理由.
【答案】
解(1)由 得
得
当 时,
时,
即 (由题意可知
(由题意可知 ).
).
 是公比为
是公比为 的等比数列,而
的等比数列,而
 (3分)
(3分)
由 得
得
 (6分)
(6分)
(2) 设
设 则
则
 ,①
,①
(1)-(2) ,化简得
,化简得 (10分)
(10分)
而

都随 的增大而增大,当
的增大而增大,当 时
时 ,
,
 所以所求的正整数
所以所求的正整数 存在,其最小值为2.
存在,其最小值为2.
【解析】略

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 的前
的前 项和
项和 和通项
和通项 满足
满足 (
( 是常数且
是常数且 )。
)。 时,试证明
时,试证明 ;
; (Ⅲ)设函数
(Ⅲ)设函数 ,
, ,是否存在正整数
,是否存在正整数 ,使
,使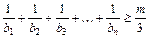 对
对 都成立?若存在,求出
都成立?若存在,求出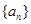 的前
的前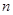 项和
项和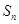 和通项
和通项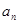 满足
满足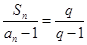 (
(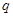 是常数且
是常数且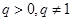 )。
)。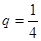 时,试证明
时,试证明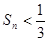 ;
;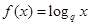 ,
, ,是否存在正整数
,是否存在正整数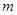 ,使
,使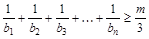 对
对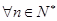 都成立?若存在,求出
都成立?若存在,求出