题目内容
已知数列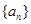 的前
的前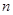 项和
项和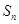 和通项
和通项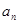 满足
满足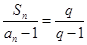 (
(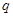 是常数且
是常数且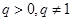 )。
)。
(Ⅰ)求数列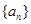 的通项公式;
的通项公式;
(Ⅱ) 当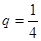 时,试证明
时,试证明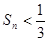 ;
;
(Ⅲ)设函数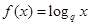 ,
, ,是否存在正整数
,是否存在正整数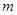 ,使
,使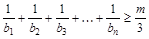 对
对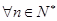 都成立?若存在,求出
都成立?若存在,求出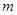 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】
(1)
(2)略
(3)1,2,3
【解析】解: (Ⅰ)由题意, ,得
,得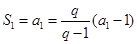
 ∴
∴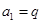 …………1分
…………1分
当 时,
时,  ,
,
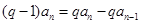 ∴
∴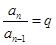 ………………3分
………………3分
∴数列 是首项
是首项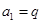 ,公比为
,公比为 的等比数列,∴
的等比数列,∴ ………4分
………4分
(Ⅱ)由(Ⅰ)知当 时,
时, …………………5分
…………………5分
∵ ,∴
,∴ …………………………………………………6分
…………………………………………………6分
即 …………………………………………………………………………7分
…………………………………………………………………………7分
(Ⅲ)∵ 
 =
=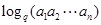
= ……………………9分
……………………9分
∵ ………………………………10分
………………………………10分
∴

 =
= …12分
…12分
由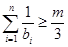 得
得
 -------(
-------(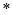 )
)
∵(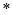 )对
)对 都成立 ∴
都成立 ∴ ∵
∵ 是正整数,∴
是正整数,∴ 的值为1,2,3。
的值为1,2,3。
∴使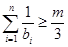 对
对 都成立的正整数
都成立的正整数 存在,其值为:1,2,3. …14分
存在,其值为:1,2,3. …14分

练习册系列答案
相关题目
 的前
的前 项和
项和 和通项
和通项 满足
满足 (
( 是常数且
是常数且 )。
)。 时,试证明
时,试证明 ;
; (Ⅲ)设函数
(Ⅲ)设函数 ,
, ,是否存在正整数
,是否存在正整数 ,使
,使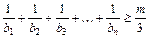 对
对 都成立?若存在,求出
都成立?若存在,求出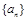 的前
的前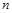 项和
项和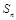 和通项
和通项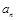 满足
满足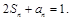 数列
数列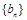 中,
中,
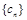 满足
满足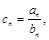 是否存在正整数
是否存在正整数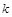 ,使得
,使得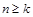 时
时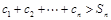 恒成立?若存在,求
恒成立?若存在,求