题目内容
已知函数f（x）=
，g（x）=lnx，则函数y=f（x）-g（x）的零点个数为（ ）
|
| A、1 | B、2 | C、3 | D、4 |
考点：根的存在性及根的个数判断
专题：数形结合,函数的性质及应用
分析：画出f（x）=
，g（x）=lnx的图象，根据图形可判断交点个数．
|
解答：
解：∵f（x）=
，g（x）=lnx，
∴根据图形可判断：有3个交点，
∴函数y=f（x）-g（x）的零点个数为3个，
故选：C
解：∵f（x）=
|
∴根据图形可判断：有3个交点，
∴函数y=f（x）-g（x）的零点个数为3个，
故选：C
点评：本他考查了函数图象的运用求解有关系的函数的零点问题，关键是化函数图象，属于中档题．
练习册系列答案
相关题目
已知抛物线的一条过焦点F的弦PQ，点R在直线PQ上，且满足
=
(
+
)，R在抛物线准线上的射影为S，设α，β是△PQS中的两个锐角，则下列四个式子
①tanαtanβ=1；②sinα+sinβ≤
；③cosα+cosβ＞1；④|tan（α-β）|＞tan
中一定正确的有（ ）
| OR |
| 1 |
| 2 |
| OP |
| OQ |
①tanαtanβ=1；②sinα+sinβ≤
| 2 |
| α+β |
| 2 |
中一定正确的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
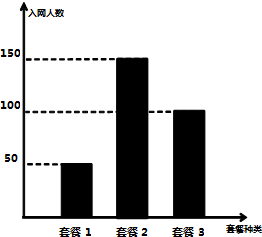移动公司在国庆期间推出4G套餐，对国庆节当日办理套餐的客户进行优惠，优惠方案如下：选择套餐一的客户可获得优惠200元，选择套餐二的客户可获得优惠500元，选择套餐三的客户可获得优惠300元．国庆节当天参与活动的人数统计结果如图所示，现将频率视为概率．△ABC的内角A，B，C的对边分别为a，b，c，若a，b，c成等比数列，且c=2a，则sinB=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知θ∈（0，
），则
+
的最小值为（ ）
| π |
| 2 |
| 2 |
| sinθ |
| 3 |
| 1-sinθ |
A、5+2
| ||
| B、10 | ||
C、6+2
| ||
D、6+5
|
