已知直线l:ax+y-4=0过点.则直线l的斜率为( )A．-3B．3C．-2D．2 题目和参考答案——青夏教育精英家教网—

题目内容

7．已知直线l：ax+y-4=0过点（-1，2），则直线l的斜率为（　　）

A．

-3

B．

C．

-2

D．

分析根据题意，由直线过点（-1，2），可得a×（-1）+2-4=0，解可得a=-2，即可得直线的方程，将直线方程化为斜截式，由斜截式的定义即可得答案．

解答解：根据题意，直线l：ax+y-4=0过点（-1，2），
则有a×（-1）+2-4=0，解可得a=-2，
即直线l的方程为：-2x+y-4=0，变形可得y=2x+4，
则直线l的斜率为2；
故选：D．

点评本题考查直线的斜率，注意要先求出直线的方程，属于基础题．

练习册系列答案

相关题目

17．

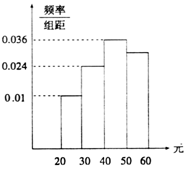为了倡导人民群众健康的生活方式，某社区服务中心通过网站对岁的社区居民随机抽取n人进行了调查，得到如下各年龄段人数频率分布直方图，若该公司决定在各年龄段用分层抽样抽取50名观众进行奖励，则年龄段[50，60]的获奖人数为（　　）

18．“a≤0”是“函数f（x）=|x（ax+1）|在区间（-∞，0）内单调递减”的（　　）

	A．	充分不必要条件		B．	必要不充分条件
	C．	充分必要条件		D．	既不充分也不必要条件

15．若连续抛掷一枚骰子两次，第一次得到的点数为m，第二次得到的点数为n，则点P（m，n）落在以坐标原点为圆心，4为半径的圆内的概率为$\frac{2}{9}$．

2．幂函数y=f（x）的图象经过点$（3，\root{3}{3}）$，则f（x）是（　　）

	A．	偶函数，且在（0，+∞）上是增函数
	B．	偶函数，且在（0，+∞）上是减函数
	C．	奇函数，且在（0，+∞）上是增函数
	D．	非奇非偶函数，且在（0，+∞）上是增函数

12．已知函数f（x）=x³-px²-qx的图象与x轴切于（1，0）点，则f（x）在[-1，1]的最大值、最小值分别为（　　）

19．某工厂在甲、乙两地的两个分厂各生产某种机器12台和6台，现销售给A地10台，B地8台，已知从甲地调动1台至A地和B地的运费分别为4百元和8百元，从乙地调运1台至A地和B地的费用分别为3百元和5百元．
（Ⅰ）设从乙地调运x台至A地，求总费用y关于台数x的函数解析式；
（Ⅱ）若总运费不超过90百元，问共有几种调运方案；
（Ⅲ）求出总运费最低的调运方案及最低的运费．

16．设a=2^2.5，b=log${\;}_{\frac{1}{2}}$2.5，c=（$\frac{1}{2}$）^2.5，则a，b，c之间的大小关系是（　　）

6．已知向量$\overrightarrow{a}$=（sinθ，cosθ），$\overrightarrow{b}$=（1，$\sqrt{3}$），满足$\overrightarrow{a}$•$\overrightarrow{b}$=2，求tanθ的值．

试题分类