题目内容
16.已知函数f(x)=2x,g(x)=-$\frac{3x-1}{x}$,则f(x)•g(x)=2-6x,(x≠0).分析 f(x)•g(x)=(-$\frac{3x-1}{x}$)(2x),其定义域为f(x)与g(x)的交集.
解答 解:函数f(x)=2x,定义域为R,
g(x)=-$\frac{3x-1}{x}$,定义域为{x∈R|x≠0}
那么:f(x)•g(x)=(-$\frac{3x-1}{x}$)(2x)=2-6x,其定义域为{x|x≠0}.
故答案为:2-6x,(x≠0).
点评 本题考查了函数解析式的求法,注意定义域的范围问题,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.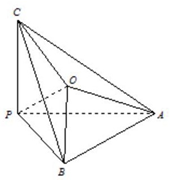 如图,在三棱锥P-ABC中,∠APB=∠BPC=∠APC=90°,O在△ABC内,∠OPC=45°,∠OPA=60°,则∠OPB的余弦值为( )
如图,在三棱锥P-ABC中,∠APB=∠BPC=∠APC=90°,O在△ABC内,∠OPC=45°,∠OPA=60°,则∠OPB的余弦值为( )
 如图,在三棱锥P-ABC中,∠APB=∠BPC=∠APC=90°,O在△ABC内,∠OPC=45°,∠OPA=60°,则∠OPB的余弦值为( )
如图,在三棱锥P-ABC中,∠APB=∠BPC=∠APC=90°,O在△ABC内,∠OPC=45°,∠OPA=60°,则∠OPB的余弦值为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
11.设函数$f(x)=\left\{\begin{array}{l}{log}_{\frac{1}{2}}^{(-x)},x<0\\{log}_{2}^{x},x>0\end{array}\right.$,若f(a)>f(-a),则a的范围为( )
| A. | (-1,0)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1)∪(0,1) |
1.若a1、b1、c1、a2、b2、c2∈R,且都不为零,则“$\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$”是“关于x的不等式a1x2+b1x+c1>0与a2x2+b2x+c2>0的解集相同”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
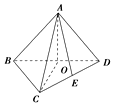 在四面体A-BCD中,AB=BC=CD=AD,∠BAD=∠BCD=90°,二面角A-BD-C为直二面角,E是CD的中点,则∠AED的度数为90°.
在四面体A-BCD中,AB=BC=CD=AD,∠BAD=∠BCD=90°,二面角A-BD-C为直二面角,E是CD的中点,则∠AED的度数为90°.