题目内容
14.设${a_n}={n^2}-2kn+6$(n∈N*,k∈R)(1)证明:k≤1是{an}为递增数列的充分不必要条件;
(2)若$?n∈{N^*},\frac{a_n}{n}≥1$,求k的取值范围.
分析 (1)an+1-an>0,解得k<$\frac{2n+1}{2}$,进而证明.
(2)$?n∈{N^*},\frac{a_n}{n}≥1$,可得$n+\frac{6}{n}$≥2k+1,利用数列的单调性即可得出.
解答 (1)证明:an+1-an=(n+1)2-2k(n+1)+6-[n2-2kn+6]=2n+1-2k>0,解得k<$\frac{2n+1}{2}$,
∴k<$\frac{3}{2}$.
∴k≤1是{an}为递增数列的充分不必要条件;
(2)解:∵$?n∈{N^*},\frac{a_n}{n}≥1$,
∴$n+\frac{6}{n}$-2k≥1,即$n+\frac{6}{n}$≥2k+1,
∵$n+\frac{6}{n}$≥5,
∴2k+1≤5,
∴k≤2.
∴k的取值范围是k≤2.
点评 本题考查了数列的单调性、充要条件的判定、恒成立问题,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.已知函数$f(x)=\left\{\begin{array}{l}{2^{-x}}+1,x≤0\\{log_3}x+ax,x>0\end{array}\right.$,若f(f(-1))>4a,则实数a的取值范围是( )
| A. | (-∞,1) | B. | (-∞,0) | C. | $(-∞,-\frac{1}{5})$ | D. | (1,+∞) |
5.已知向量$\overrightarrow a$,$\overrightarrow b$满足$|{\overrightarrow a}|=2$,$|{\overrightarrow b}|=1$且$({\overrightarrow a+\overrightarrow b})⊥\overrightarrow b$,则$\overrightarrow a$与$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{6}$ |
9.当-1≤x≤1,函数y=2x-2的值域为( )
| A. | [-$\frac{3}{2}$,0] | B. | [0,$\frac{3}{2}$] | C. | [-1,0] | D. | [-$\frac{3}{2}$,1] |
6.小军旅行箱的密码是一个六位数,由于他忘记了密码的末位数字,则小军能一次打开该旅行箱的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{5}$ |
4.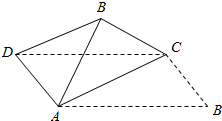 如图,将矩形纸片ABCD(其中$AB=\sqrt{3}$,BC=1)沿对角线AC折起后,使得异面直线BC⊥AD,则此时异面直线AB和CD所成的角的余弦值是( )
如图,将矩形纸片ABCD(其中$AB=\sqrt{3}$,BC=1)沿对角线AC折起后,使得异面直线BC⊥AD,则此时异面直线AB和CD所成的角的余弦值是( )
 如图,将矩形纸片ABCD(其中$AB=\sqrt{3}$,BC=1)沿对角线AC折起后,使得异面直线BC⊥AD,则此时异面直线AB和CD所成的角的余弦值是( )
如图,将矩形纸片ABCD(其中$AB=\sqrt{3}$,BC=1)沿对角线AC折起后,使得异面直线BC⊥AD,则此时异面直线AB和CD所成的角的余弦值是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
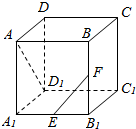 长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=a,E和F分别是A1B1和BB1的中点,求:
长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=a,E和F分别是A1B1和BB1的中点,求: