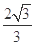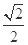题目内容
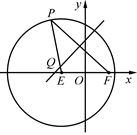
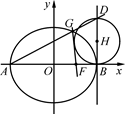
如图,已知圆E 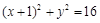 ,点
,点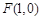 ,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
(1)求动点Q的轨迹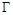 的方程;
的方程;
(2)点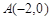 ,
,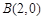 ,点G是轨迹
,点G是轨迹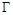 上的一个动点,直线AG与直线
上的一个动点,直线AG与直线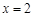 相交于点D,试判断以线段BD为直径的圆与直线GF的位置关系,并证明你的结论.
相交于点D,试判断以线段BD为直径的圆与直线GF的位置关系,并证明你的结论.
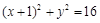 ,点
,点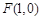 ,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.(1)求动点Q的轨迹
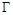 的方程;
的方程;(2)点
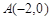 ,
,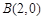 ,点G是轨迹
,点G是轨迹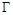 上的一个动点,直线AG与直线
上的一个动点,直线AG与直线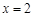 相交于点D,试判断以线段BD为直径的圆与直线GF的位置关系,并证明你的结论.
相交于点D,试判断以线段BD为直径的圆与直线GF的位置关系,并证明你的结论.
(1)点Q的轨迹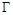 的方程为为
的方程为为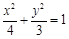 .(2)以线段BD为直径的圆与直线GF相切.
.(2)以线段BD为直径的圆与直线GF相切.
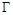 的方程为为
的方程为为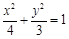 .(2)以线段BD为直径的圆与直线GF相切.
.(2)以线段BD为直径的圆与直线GF相切.试题分析:(1)连结QF,由于线段的垂直平分线上的点到线段两端点的距离相等,所以|QE|+|QF|=|QE|+|QP|=4
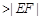 ,根据椭圆的定义知,动点Q的轨迹
,根据椭圆的定义知,动点Q的轨迹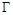 是以E,F为焦点,长轴长为4的椭圆.由此便可得其方程;(2)直线与圆的位置关系一般通过比较圆心到直线的距离与圆的半径的大小关系来确定. 由题意,设直线AG的方程为
是以E,F为焦点,长轴长为4的椭圆.由此便可得其方程;(2)直线与圆的位置关系一般通过比较圆心到直线的距离与圆的半径的大小关系来确定. 由题意,设直线AG的方程为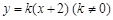 ,则点D坐标为
,则点D坐标为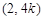 ,由此可得圆心和半径.下面用k表示点G的坐标,求出直线GF方程为
,由此可得圆心和半径.下面用k表示点G的坐标,求出直线GF方程为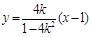 ,进而求到圆心到直线GF的距离便可知道以BD为直径的圆与直线GF的位置关系.
,进而求到圆心到直线GF的距离便可知道以BD为直径的圆与直线GF的位置关系.(1)连结QF,根据题意,|QP|=|QF|,
则|QE|+|QF|=|QE|+|QP|=4
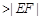 ,
,故Q的轨迹
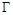 是以E,F为焦点,长轴长为4的椭圆. .2分
是以E,F为焦点,长轴长为4的椭圆. .2分设其方程为
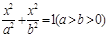 ,可知
,可知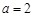 ,
,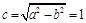 ,则
,则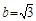 , ..3分
, ..3分所以点Q的轨迹
 的方程为为
的方程为为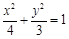 . 4分
. 4分(2)以线段BD为直径的圆与直线GF相切. 5分
由题意,设直线AG的方程为
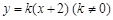 ,则点D坐标为
,则点D坐标为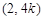 ,BD的中点H的坐标为
,BD的中点H的坐标为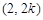 .
.联立方程组
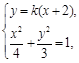 消去y得
消去y得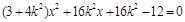 ,
,设
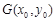 ,则
,则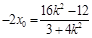 ,
,所以
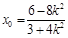 ,
,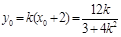 , 7分
, 7分当
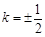 时,点G的坐标为
时,点G的坐标为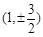 ,点D的坐标为
,点D的坐标为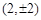 .
.直线GF⊥x轴,此时以BD为直径的圆
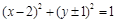 与直线GF相切. 9分
与直线GF相切. 9分当
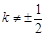 时,则直线GF的斜率为
时,则直线GF的斜率为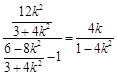 ,则直线GF方程为
,则直线GF方程为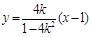 ,
,点H到直线GF的距离
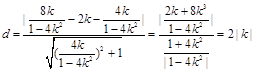 ,又
,又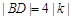 ,
,所以圆心H到直线GF的距离
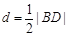 ,此时,以BD为直径的圆与直线GF相切.
,此时,以BD为直径的圆与直线GF相切.综上所述,以线段BD为直径的圆与直线GF相切. 13分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .称圆心在原点O,半径为
.称圆心在原点O,半径为 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为 ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为 .
. ,使得
,使得 与椭圆C都只有一个交点,试判断
与椭圆C都只有一个交点,试判断 的中心和抛物线
的中心和抛物线 的顶点均为原点
的顶点均为原点 ,
,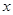 轴上,过
轴上,过 ,与
,与

 为
为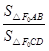 的最小值;
的最小值; 是
是 ,求证:
,求证: 为定值;反之,当
为定值;反之,当 是椭圆
是椭圆 的一个顶点,
的一个顶点, 的长轴是圆
的长轴是圆 的直径,
的直径, 、
、 是过点
是过点 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中 于
于 、
、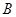 两点,
两点,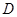 .
.
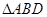 面积的最大值及取得最大值时直线
面积的最大值及取得最大值时直线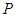 是椭圆
是椭圆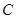 上任一点,点
上任一点,点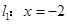 的距离为
的距离为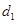 ,到点
,到点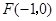 的距离为
的距离为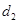 ,且
,且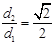 .直线
.直线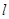 与椭圆
与椭圆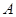 、
、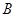 (
(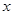 轴上方),且
轴上方),且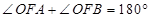 .
.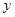 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线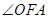 如何变化,直线
如何变化,直线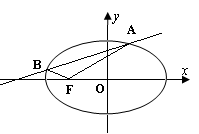
 (a>b>0)的左、右焦点,若在直线x=
(a>b>0)的左、右焦点,若在直线x= 上存在P,使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( )
上存在P,使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( )



 的右焦点为F(3,0),过点F的直线交椭圆E于A、B两点.若AB的中点坐标为(1,﹣1),则E的方程为( )
的右焦点为F(3,0),过点F的直线交椭圆E于A、B两点.若AB的中点坐标为(1,﹣1),则E的方程为( )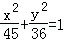 B.
B.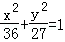
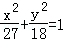 D.
D.
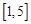 和
和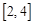 上分别取一个数,记为
上分别取一个数,记为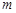 和
和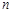 ,则方程
,则方程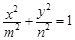 ,表示焦点在y轴上的椭圆的概率是 .
,表示焦点在y轴上的椭圆的概率是 .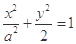 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,则该椭圆的离心率是( )
的焦点重合,则该椭圆的离心率是( )