题目内容
20. 如图,四棱锥C-ABED中,四边形ABED是正方形,若G,F分别是线段EC,BD的中点.
如图,四棱锥C-ABED中,四边形ABED是正方形,若G,F分别是线段EC,BD的中点.(1)求证:GF∥底面ABC;
(2)若点P为线段CD的中点,平面GFP与平面ABC有怎样的位置关系?并证明.
分析 (1)根据线面平行的判定定理,证明GF平行于平面ABC内的一条直线AC即可;
(2)根据面面平行的判定定理,因为GF∥平面ABC,只要证明FP∥平面ABC,问题得以解决.
解答  解:(1)证明:连接AE,由F是线段BD的中点得F为AE的中点,
解:(1)证明:连接AE,由F是线段BD的中点得F为AE的中点,
∴GF为△AEC的中位线,
∴GF∥AC,
又∵AC?平面ABC,GF?平面ABC
∴GF∥平面ABC,
(2)平面GFE∥平面ABC,
证明如下:
∵F,P分别为BD,CD的中点,
∴FP为△BCD的中位线,
∴FP∥BC,
又∵BC?平面ABC,FP?平面ABC,
∴FP∥平面ABC,
又GF∥平面ABC,FP∩GF=F,FP?平面FPG,GF?平面FPG
∴平面GFP∥平面ABC.
点评 本题考查了直线与平面平行,平面与平面平行的判断问题,关键是掌握定理,属于中档题.

练习册系列答案
相关题目
8.非零向量$\overrightarrow{a}$,$\overrightarrow{b}$夹角为120°,且|$\overrightarrow{a}$-$\overrightarrow{b}$|=1,则|$\overrightarrow{a}$+$\overrightarrow{b}$|的取值范围为( )
| A. | (1,$\sqrt{3}$] | B. | [$\frac{\sqrt{3}}{3}$,1) | C. | ($\frac{\sqrt{3}}{3}$,1) | D. | [$\frac{\sqrt{3}}{3}$,3] |
15.已知椭圆$\frac{x^2}{4}+{y^2}=1$的焦点为F1,F2,若点 P在椭圆上,则满足|P O|2=|PF1|•|PF2|(其中 O为坐标原点)的点 P有( )
| A. | 无数个 | B. | 6个 | C. | 4个 | D. | 0个 |
5.已知双曲线x${\;}^{2}-\frac{{y}^{2}}{{b}^{2}}=1$(b>0),若右焦点F(c,0)到一条渐近线的距离为2,则双曲线的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\sqrt{5}$ |
12.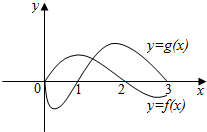 已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-3,3],且它们在x∈[0,3]上的图象如图所示,则不等式f(x)•g(x)<0的解集是( )
已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-3,3],且它们在x∈[0,3]上的图象如图所示,则不等式f(x)•g(x)<0的解集是( )
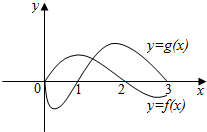 已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-3,3],且它们在x∈[0,3]上的图象如图所示,则不等式f(x)•g(x)<0的解集是( )
已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-3,3],且它们在x∈[0,3]上的图象如图所示,则不等式f(x)•g(x)<0的解集是( )| A. | (0,1)∪(2,3) | B. | (-2,-1)∪(0,1)∪(2,3) | ||
| C. | (-1,0)∪(-3,-2)∪(0,1)∪(2,3) | D. | (-3,-1)∪(0,1)∪(2,3) |
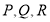 是圆
是圆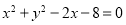 上不同三点,它们到直线
上不同三点,它们到直线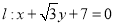 的距离分别为
的距离分别为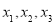 ,若
,若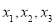 成等差数列,则公差的最大值为( )
成等差数列,则公差的最大值为( )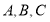 是双曲线
是双曲线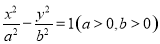 上的三个点,
上的三个点,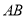 经过原点
经过原点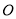 ,
,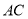 经
经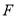 ,若
,若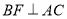 且
且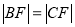 ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )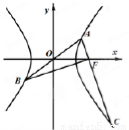
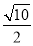 B.
B.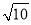 C.
C.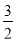 D.
D.