题目内容
13.一个圆锥的底面半径为2cm,高为6cm,其中有一个高为xcm的内接圆柱.(1)求圆锥的侧面积;
(2)当x为何值时,圆柱的侧面积最大?并求出最大值.
分析 (1)求出圆锥的母线长,利用侧面积公式求解即可.
(2)由(1)由题意作出几何体的轴截面,根据轴截面和比例关系列出方程,求出圆柱的底面半径,再表示出圆柱的侧面积;根据基本不等式求出侧面面积的最大值.
解答 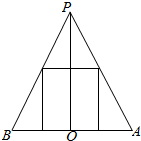 解:(1)母线长为:$\sqrt{{6}^{2}+{2}^{2}}$=$2\sqrt{10}$(cm),所以圆锥的侧面积S=πrl=4$\sqrt{10}π$.(cm2).
解:(1)母线长为:$\sqrt{{6}^{2}+{2}^{2}}$=$2\sqrt{10}$(cm),所以圆锥的侧面积S=πrl=4$\sqrt{10}π$.(cm2).
(2)设所求的圆柱的底面半径为r,它的轴截面如图:
由图得,$\frac{r}{2}$=$\frac{6-x}{6}$,即r=2-$\frac{x}{3}$.
∴S圆柱侧=2πrx=2π(2-$\frac{x}{3}$)x=4πx-$\frac{2π}{3}$x2≤$\frac{2}{3}[\frac{(6-x)+x}{2}]^{2}π$=6π
当且仅当x=3时取等号,∴当圆柱的高为3cm时,它的侧面积最大为6πcm2(10分).
点评 本题的考点是简单组合体的面积问题,关键是作出轴截面,求出长度之间的关系式,表示出面积后利用函数的思想求出最值,考查了数形结合思想和函数思想.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
1.“a>b”是“2a>2b”( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
8.非零向量$\overrightarrow{a}$,$\overrightarrow{b}$夹角为120°,且|$\overrightarrow{a}$-$\overrightarrow{b}$|=1,则|$\overrightarrow{a}$+$\overrightarrow{b}$|的取值范围为( )
| A. | (1,$\sqrt{3}$] | B. | [$\frac{\sqrt{3}}{3}$,1) | C. | ($\frac{\sqrt{3}}{3}$,1) | D. | [$\frac{\sqrt{3}}{3}$,3] |
5.已知双曲线x${\;}^{2}-\frac{{y}^{2}}{{b}^{2}}=1$(b>0),若右焦点F(c,0)到一条渐近线的距离为2,则双曲线的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\sqrt{5}$ |
3.函数f(x)=lg(3x-1)的定义域为( )
| A. | y=lnx | B. | (0,+∞) | C. | R | D. | ($\frac{1}{3}$,+∞) |
 在平面
在平面 内,过点
内,过点 和
和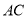 ,应该怎样画线?
,应该怎样画线?
 的前
的前 项和为
项和为 ,
, ,且
,且 成等比数列.
成等比数列. 的通项公式;
的通项公式; ,求数列
,求数列 的前
的前 .
.