题目内容
如图,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2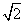 ,C1H⊥平面AA1B1B,且C1H=
,C1H⊥平面AA1B1B,且C1H=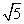 .
.
(1)求异面直线AC与A1B1所成角的余弦值;
(2) 设N为棱B1C1的中点,点M在平面AA1B1B内,且MN⊥平面A1B1C1,求线段BM的长.

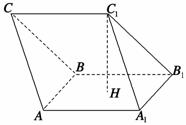
[解析] 如图所示 ,建立空间直角坐标系,点B为坐标原点.依题意得A(2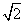 ,0,0),B(0,0,0),C(
,0,0),B(0,0,0),C(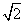 ,-
,-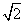 ,
,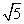 ),A1(2
),A1(2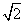 ,2
,2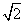 ,0),B1(0,2
,0),B1(0,2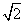 ,0),C1(
,0),C1(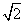 ,
,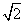 ,
,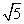 ).
).

不妨令y=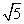 ,可得n=(0,
,可得n=(0,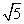 ,
,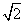 ).
).
于是cos〈m,n〉= =
= =
= ,
,
从而sin〈m,n〉= .
.
所以二面角A-A1C1-B1的正弦值为 .
.

所以线段BM的长| |=
|= .
.

练习册系列答案
相关题目
 行有
行有 个数(从左数起)记为
个数(从左数起)记为 ,
,
 为地震时所散发出来的相对能量程度,则里氏震级量度
为地震时所散发出来的相对能量程度,则里氏震级量度 可定义为
可定义为 则日本9.0级地震和汶川8.0级地震的相对能量的比值
则日本9.0级地震和汶川8.0级地震的相对能量的比值 .(精确到整数)
.(精确到整数)  ).
). B.0 C.
B.0 C. ,等比数列3,
,等比数列3, ,则该等差数列的公差为 ( )
,则该等差数列的公差为 ( ) B.3或
B.3或 C.3 D.
C.3 D. }的前n项和
}的前n项和 满足:
满足: ,且
,且 =1.那么
=1.那么 =( )
=( ) ,
, 和直线
和直线 围成的图形面积是 ( )
围成的图形面积是 ( )  B.
B.  C.
C.  D.
D. 
 ,求
,求