题目内容
已知函数f（x）=x|x-m|，x∈R．且f（4）=0，
（1）求实数m的值．
（2）作出函数f（x）的图象．
（3）根据图象写出f（x）的单调区间，写出不等式f（x）＞0的解集．
（1）求实数m的值．
（2）作出函数f（x）的图象．
（3）根据图象写出f（x）的单调区间，写出不等式f（x）＞0的解集．
考点：函数的图象,函数单调性的性质,函数的值
专题：函数的性质及应用
分析：（1）代入值求的即可．
（2）化为分段函数，作图即可，
（3）由图象直接观察出单调区间以及不等式f（x）＞0的解集．
（2）化为分段函数，作图即可，
（3）由图象直接观察出单调区间以及不等式f（x）＞0的解集．
解答：
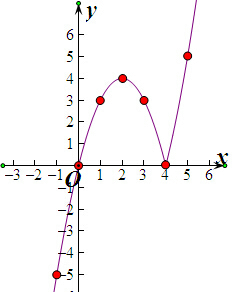解：（1）∵f（4）=0，
∴f（4）=4|4-m|=0，
∴m=4，
（2）f（x）=x|x-4|=
图象如图所示
（3）由图象可知，函数f（x）在（-∞，2），（4，+∞）上单调递增，在（2，4）上单调递减．
∵f（x）＞0，由图象可知
不等式的解集为（0，4）∪（4，+∞）．
解：（1）∵f（4）=0，∴f（4）=4|4-m|=0，
∴m=4，
（2）f（x）=x|x-4|=
|
（3）由图象可知，函数f（x）在（-∞，2），（4，+∞）上单调递增，在（2，4）上单调递减．
∵f（x）＞0，由图象可知
不等式的解集为（0，4）∪（4，+∞）．
点评：本题主要考查了分段函数的画法和由图象得到有关单调区间以及不等式的解集，属于基础题．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
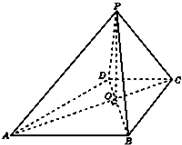如图，已知四棱锥P-ABCD的底面ABCD为等腰梯形，AB∥DC，AC⊥BD，AC与BD相交于点O，且顶点P在底面上的射影恰为O点，又BO=2，PO=