题目内容
已知函数f(x)=2sin(2x+φ)(0<φ<2π)的图象过点(
,-2).
(1)求φ的值;
(2)若f(
)=
,-
<α<0,求sin(2α-
)的值.
| π |
| 2 |
(1)求φ的值;
(2)若f(
| α |
| 2 |
| 6 |
| 5 |
| π |
| 2 |
| π |
| 6 |
考点:函数y=Asin(ωx+φ)的图象变换,二倍角的正弦
专题:三角函数的图像与性质
分析:(1)直接由函数f(x)=2sin(2x+φ)的图象过点(
,-2)列式求得sinφ=1,然后根据0<φ<2π得答案;
(2)由f(
)=
求得cosα=
,进一步求得sin2α,展开两角差的正弦得答案.
| π |
| 2 |
(2)由f(
| α |
| 2 |
| 6 |
| 5 |
| 3 |
| 5 |
解答:
解:(1)∵函数f(x)=2sin(2x+φ)(0<φ<2π)的图象过点(
,-2),
∴f(
)=2sin(π+φ)=-2,
即sinφ=1.
∵0<φ<2π,
∴φ=
;
(2)由(1)得,f(x)=2cos2x.
∵f(
)=
,∴cosα=
.
又∵-
<α<0,
∴sinα=-
.
∴sin2α=2sinαcosα=-
,cos2α=2cos2α-1=-
.
从而sin(2α-
)=sin2αcos
-cos2αsin
=
.
| π |
| 2 |
∴f(
| π |
| 2 |
即sinφ=1.
∵0<φ<2π,
∴φ=
| π |
| 2 |
(2)由(1)得,f(x)=2cos2x.
∵f(
| α |
| 2 |
| 6 |
| 5 |
| 3 |
| 5 |
又∵-
| π |
| 2 |
∴sinα=-
| 4 |
| 5 |
∴sin2α=2sinαcosα=-
| 24 |
| 25 |
| 7 |
| 25 |
从而sin(2α-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
7-24
| ||
| 50 |
点评:本题考查了y=Asin(ωx+φ)型函数的图象和性质,训练了由已知三角函数的值求三角函数的值,是中档题.

练习册系列答案
相关题目
已知随机变量ξ服从正态分布N(1,4),若P(ξ>2)=a,则P(0<ξ<1)=( )
| A、a | ||
| B、1-a | ||
| C、2a-1 | ||
D、
|
已知x,y,z∈R+,且x+4y+9z=1,则
+
+
的最小值是( )
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
| A、9 | B、16 | C、36 | D、81 |
 某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图所示部分频率分布直方图.观察图形给出的信息,回答下列问题:
某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图所示部分频率分布直方图.观察图形给出的信息,回答下列问题: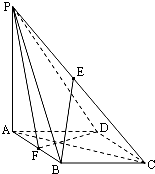 如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PA=2,PA⊥平面ABCD,E是PC的中点,F是AB中点.
如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PA=2,PA⊥平面ABCD,E是PC的中点,F是AB中点.