题目内容
针对时下的“韩剧热”,某校团委对“学生性别和喜欢韩剧是否有关”作了一次调查,其中女生人数是男生人数的
,男生喜欢韩剧的人数占男生人数的
,女生喜欢韩剧人数占女生人数的
.
(1)若在犯错误的概率不超过0.05的前提下认为是否喜欢韩剧和性别有关,则男生至少有多少人;
(2)若没有充分的证据显示是否喜欢韩剧和性别有关,则男生至多有多少人.
附临界值参考表:
| 1 |
| 2 |
| 1 |
| 6 |
| 2 |
| 3 |
(1)若在犯错误的概率不超过0.05的前提下认为是否喜欢韩剧和性别有关,则男生至少有多少人;
(2)若没有充分的证据显示是否喜欢韩剧和性别有关,则男生至多有多少人.
附临界值参考表:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
考点:独立性检验的应用
专题:应用题,概率与统计
分析:(1)设男生人数为x,依题意可得列联表;根据所给的表格中的数据,代入求观测值的公式,求出观测值同临界值进行比较,即可得出结论;
(2)由k=
=
x≤3.841,解得x≤10.24,即可得出结论.
(2)由k=
| ||||||
|
| 3 |
| 8 |
解答:
解:(1)设男生人数为x,依题意可得列联表如下:
若在犯错误的概率不超过0.05的前提下认为是否喜欢韩剧和性别有关,则k>3.841,
由k=
=
x>3.841,解得x>10.24,
∵
,
为整数,
∴若在犯错误的概率不超过0.05的前提下认为是否喜欢韩剧和性别有关,则男生至少有12人;
(2)由k=
=
x≤3.841,解得x≤10.24,
∵
,
为整数,
∴若没有充分的证据显示是否喜欢韩剧和性别有关,则男生至多有6人.
| 喜欢韩剧 | 不喜欢韩剧 | 总计 | |||||||
| 男生 |
|
| x | ||||||
| 女生 |
|
|
| ||||||
| 总计 |
| x |
|
由k=
| ||||||
|
| 3 |
| 8 |
∵
| x |
| 2 |
| x |
| 6 |
∴若在犯错误的概率不超过0.05的前提下认为是否喜欢韩剧和性别有关,则男生至少有12人;
(2)由k=
| ||||||
|
| 3 |
| 8 |
∵
| x |
| 2 |
| x |
| 6 |
∴若没有充分的证据显示是否喜欢韩剧和性别有关,则男生至多有6人.
点评:本题考查独立性检验知识,考查学生的计算能力,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
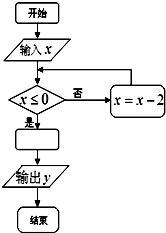 如图是一个算法程序框图,当输入的x值为3时,输出的结果恰好是
如图是一个算法程序框图,当输入的x值为3时,输出的结果恰好是| 1 |
| 3 |
A、y=x -
| ||
B、y=x
| ||
| C、y=3-x | ||
| D、y=3x |