题目内容
若存在正数x使
＜1成立，则实数m的取值范围是 ．
|
考点：二阶行列式的定义,其他不等式的解法
专题：计算题,矩阵和变换
分析：化
＜1为2xx-2xm＜1，从而可得m＞x-2-x，从而解得．
|
解答：
解：
＜1可化为
2xx-2xm＜1，
故x-m＜2-x，
则m＞x-2-x，
令f（x）=x-2-x，分析易得f（x）为增函数，
而x＞0，则f（x）min=-1，
故m∈（-1，+∞）．
故答案为：（-1，+∞）．
|
2xx-2xm＜1，
故x-m＜2-x，
则m＞x-2-x，
令f（x）=x-2-x，分析易得f（x）为增函数，
而x＞0，则f（x）min=-1，
故m∈（-1，+∞）．
故答案为：（-1，+∞）．
点评：本题考查了行列式的运算及存在性问题，属于基础题．
练习册系列答案
相关题目
函数y=(
)x-2的图象必过（ ）
| 1 |
| 2 |
| A、第一、三、四象限 |
| B、第二、三、四象限 |
| C、第一、二、三象限 |
| D、第一、二、四象限 |
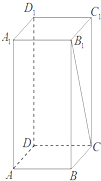如图，正四棱柱ABCD-A1B1C1D1的底面边长AB=2，若异面直线A1A与B1C所成角的大小为arctan