题目内容
1.不等式ax2+x+b>0的解集为{x|-$\frac{1}{3}<x<\frac{1}{2}$},则a+b=-5.分析 根据一元二次不等式与对应方程的关系,利用根与系数的关系求出a、b的值即可.
解答 解:∵不等式ax2+x+b>0的解集为{x|-$\frac{1}{3}<x<\frac{1}{2}$},
∴对应方程ax2+x+b=0的实数根为-$\frac{1}{3}$和$\frac{1}{2}$;
由根与系数的关系,得$\left\{\begin{array}{l}{-\frac{1}{a}=-\frac{1}{3}+\frac{1}{2}}\\{\frac{b}{a}=-\frac{1}{3}×\frac{1}{2}}\end{array}\right.$,
解得a=-6,b=1;
∴a+b=-6+1=-5.
故答案为:-5.
点评 本题考查了一元二次不等式与对应方程的应用问题,也考查了根与系数关系的应用问题,是基础题目.

练习册系列答案
相关题目
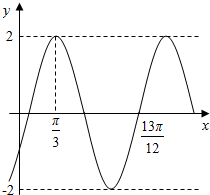 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图所示.