题目内容
根据调查,某学校开设了“街舞”、“围棋”、“武术”三个社团,三个社团参加的人数如下表所示:
为调查社团开展情况,学校社团管理部采用分层抽样的方法从中抽取一个容量为n的样本,已知从“街舞”社团抽取的同学8人.
(Ⅰ)求n的值和从“围棋”社团抽取的同学的人数;
(Ⅱ)若从“围棋”社团抽取的同学中选出2人担任该社团活动监督的职务,已知“围棋”社团被抽取的同学中有2名女生,求至少有1名女同学被选为监督职务的概率.
为调查社团开展情况,学校社团管理部采用分层抽样的方法从中抽取一个容量为n的样本,已知从“街舞”社团抽取的同学8人.
| 社团 | 街舞 | 围棋 | 武术 |
| 人数 | 320 | 240 | 200 |
(Ⅱ)若从“围棋”社团抽取的同学中选出2人担任该社团活动监督的职务,已知“围棋”社团被抽取的同学中有2名女生,求至少有1名女同学被选为监督职务的概率.
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(Ⅰ)由题意可得
=
,解方程可得n值,由比例易得所求;
(Ⅱ)由(Ⅰ)知,从“围棋”社团抽取的同学为6人,其中2位女生记为A,B,4位男生记为C,D,E,F,列举可得共15种,其中没有女生的有6种,故所求概率1-
=
| n |
| 320+240+200 |
| 8 |
| 320 |
(Ⅱ)由(Ⅰ)知,从“围棋”社团抽取的同学为6人,其中2位女生记为A,B,4位男生记为C,D,E,F,列举可得共15种,其中没有女生的有6种,故所求概率1-
| 6 |
| 15 |
| 3 |
| 5 |
解答:
解:(Ⅰ)由题意可得
=
,解得n=19,
从“围棋”社团抽取的同学240×
=6人
(Ⅱ)由(Ⅰ)知,从“围棋”社团抽取的同学为6人,
其中2位女生记为A,B,4位男生记为C,D,E,F,
则从这6位同学中任选2人,不同的结果有
{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},
{B,D},{B,E},{B,F},{C,D},{C,E},{C,F},
{D,E},{D,F},{E,F},共15种,
从这6位同学中任选2人,没有女生的有:{C,D},{C,E},
{C,F},{D,E},{D,F},{E,F},共6种
故至少有1名女同学被选中的概率1-
=
| n |
| 320+240+200 |
| 8 |
| 320 |
从“围棋”社团抽取的同学240×
| 8 |
| 320 |
(Ⅱ)由(Ⅰ)知,从“围棋”社团抽取的同学为6人,
其中2位女生记为A,B,4位男生记为C,D,E,F,
则从这6位同学中任选2人,不同的结果有
{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},
{B,D},{B,E},{B,F},{C,D},{C,E},{C,F},
{D,E},{D,F},{E,F},共15种,
从这6位同学中任选2人,没有女生的有:{C,D},{C,E},
{C,F},{D,E},{D,F},{E,F},共6种
故至少有1名女同学被选中的概率1-
| 6 |
| 15 |
| 3 |
| 5 |
点评:本题考查列举法求基本事件数以及事件发生的概率,属基础题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
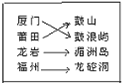 福州、厦门、莆田、龙岩四个城市,它们分别有一个著名的旅游景点鼓山、鼓浪屿、湄洲岛、龙崆洞,把福州、厦门、莆田、龙岩四个城市和它们的旅游景点鼓山、鼓浪屿、湄洲岛、龙崆洞分别写成左右两列,现在一名旅游爱好者随机用4条线把左右全部连接起来,构成“一一对应”,已知连对的得2分,连错的得0分(如图所示是一种“一一对应”的连法,连对的只有一个“厦门→鼓浪屿”).
福州、厦门、莆田、龙岩四个城市,它们分别有一个著名的旅游景点鼓山、鼓浪屿、湄洲岛、龙崆洞,把福州、厦门、莆田、龙岩四个城市和它们的旅游景点鼓山、鼓浪屿、湄洲岛、龙崆洞分别写成左右两列,现在一名旅游爱好者随机用4条线把左右全部连接起来,构成“一一对应”,已知连对的得2分,连错的得0分(如图所示是一种“一一对应”的连法,连对的只有一个“厦门→鼓浪屿”).