题目内容
过双曲线x2-
=1的左焦点F引圆x2+y2=1的切线FP交双曲线右支于点P,T为切点M为线段FP的中点,O为坐标原点,则|MO|-|MT|=( )
| y2 |
| 2 |
A、
| ||
| B、1 | ||
C、
| ||
D、
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:如图所示,设F′为双曲线的右焦点,连接PF′,OM,OT.可得OT⊥FT,FT=
=
.OM=
PF′,又|PF|-|PF′|=2a=2,利用|MO|-|MT|=
|PF′|-(
|PF|-|FT|)即可得出.
| OF2-OT2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:如图所示,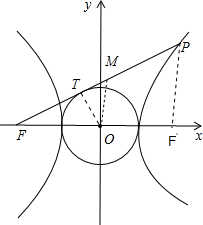
设F′为双曲线的右焦点,连接PF′,OM,OT.
∵OT⊥FT,
∴FT=
=
.
OM=
PF′,
PF-PF′=2a=2,
∴|MO|-|MT|=
|PF′|-(
|PF|-|FT|)
=|FT|+
(|PF′|-|PF|)
=
-
×2
=
-1.
故选:C.

设F′为双曲线的右焦点,连接PF′,OM,OT.
∵OT⊥FT,
∴FT=
| OF2-OT2 |
| 2 |
OM=
| 1 |
| 2 |
PF-PF′=2a=2,
∴|MO|-|MT|=
| 1 |
| 2 |
| 1 |
| 2 |
=|FT|+
| 1 |
| 2 |
=
| 2 |
| 1 |
| 2 |
=
| 2 |
故选:C.
点评:本题考查了双曲线的定义标准方程及其性质、三角形的中位线定理、圆的切线的性质、勾股定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知α∈(0,π),cos(α+
)=-
,则tan2α=( )
| π |
| 3 |
| ||
| 2 |
A、
| ||||||
B、-
| ||||||
C、-
| ||||||
D、-
|
下列函数中,在(-∞,0)上是增函数的是( )
| A、y=lgx |
| B、y=3x |
| C、y=x-1 |
| D、y=-(x+1)2 |