题目内容
9.设f(x)是奇函数,当x>0时,f(x)=x2-1,则使f(x)>0的x的取值范围x>1或-1<x<0.分析 利用函数为奇函数,将x<0转化为-x>0,再利用当x>0时,f(x)=x2-1,求得当x<0时,f(x)=-x2+1,即可求得答案.
解答 解:设x<0,则-x>0,
∵当x>0时,f(x)=x2-1,
∴f(-x)=(-x)2-1=x2-1,
又∵函数f(x)是定义在R上的奇函数,
∴f(-x)=-f(x),
∴f(x)=-f(-x)=-x2+1,
∴当x<0时,f(x)=-x2+1.
∴f(x)>0等价于$\left\{\begin{array}{l}{x>0}\\{{x}^{2}-1>0}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{-{x}^{2}+1>0}\end{array}\right.$,
∴x>1或-1<x<0,
故答案为x>1或-1<x<0.
点评 本题考查了函数解析式的求解及常用方法.对于求函数解析式的方法,一般有:待定系数法,换元法,凑配法,消元法等.本题解题的关键是运用函数的偶函数的性质,将要求的范围转化到已知的范围求解.解题时要认真审题,仔细解答,注意合理地进行等价转化.属于中档题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
3.双曲线的顶点到渐进线的距离等于虚轴长的$\frac{1}{4}$,则此双曲线的离心率是( )
| A. | 2 | B. | $\frac{3}{2}$ | C. | 3 | D. | 4 |
4.已知实数x、y满足约束条件$\left\{\begin{array}{l}{y≥1-2x}\\{y<1+x}\\{x≤2}\end{array}\right.$,则目标函数z=x+y取不到的值是( )
| A. | 1 | B. | 3 | C. | 7 | D. | 4 |
1.已知复数z满足(1+2i)z=5,则复数z的虚部等于( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
14.已知函数$f(x)={log_9}({9^x}+1)-\frac{1}{2}x$的图象与直线y=$\frac{1}{2}$x+b没有交点,则b的取值范围是( )
| A. | (-∞,0] | B. | (-∞,1] | C. | (0,1) | D. | (1,+∞) |
18.已知实数a,b满足0<a<1,-1<b<1,则函数y=$\frac{1}{3}$ax3+ax2+b有三个零点的概率为( )
| A. | $\frac{5}{16}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{11}{16}$ |
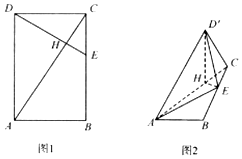 如图1,已知矩形ABCD中,$AB=2,BC=2\sqrt{3}$,点E是边BC上的点,且$CE=\frac{1}{3}CB$,DE与AC相交于点H.现将△ACD沿AC折起,如图2,点D的位置记为D',此时$D'E=\frac{{\sqrt{30}}}{3}$.
如图1,已知矩形ABCD中,$AB=2,BC=2\sqrt{3}$,点E是边BC上的点,且$CE=\frac{1}{3}CB$,DE与AC相交于点H.现将△ACD沿AC折起,如图2,点D的位置记为D',此时$D'E=\frac{{\sqrt{30}}}{3}$.