题目内容

12．如图所示，在长方体ABCD-A1B1C1D1中，E，F分别是棱AA1和棱CC1的中点．求证：EB1∥DF，ED∥B1F．（提示：设G是DD1的中点，分别连接EG，GC1）

分析 设G是DD1的中点，分别连接EG，GC1，推导出DFC1G是平行四边形，EB1C1G是平行四边形，从而DFB1E是平行四边形，由此能证明EB1∥DF，ED∥B1F．

解答 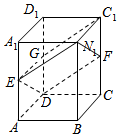证明：设G是DD1的中点，分别连接EG，GC1
∵在长方体ABCD-A1B1C1D1中，E，F分别是棱AA1和棱CC1的中点，
∴DG$\underset{∥}{=}$FC1，∴DFC1G是平行四边形，
∴GC1$\underset{∥}{=}$DF，
又EG$\underset{∥}{=}$B1C1，∴EB1C1G是平行四边形，
∴GC1$\underset{∥}{=}$EB1，
∴EB1$\underset{∥}{=}$DF，∴DFB1E是平行四边形，
∴EB1∥DF，ED∥B1F．

点评 本题考查直线与直线平行的证明，是中档题，解题时要认真审题，注意平行公理的合理运用．

练习册系列答案
相关题目
2．我国数学史上有一部堪与欧几里得《几何原本》媲美的书，这就是历来被尊为算经之首的《九章算术》，其中卷第五《商功》有一道关于圆柱体的体积试题：今有圆堡，周四丈八尺，高一丈一尺，问积几何？其意思是：含有圆柱形的土筑小城堡，底面周长是4丈8尺，高1丈1尺，问它的体积是多少？若π取3，估算小城堡的体积为（　　）
A．1998立方尺B．2012立方尺C．2112立方尺D．2324立方尺
3．某校高一年级学生全部参加了体育科目的达标测试，现从中随机抽取40名学生的测试成绩，整理数据并按分数段[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]进行分组，假设同一组中的每个数据可用该组区间的中点值代替，则得到体育成绩的折线图（如下）

（Ⅰ）体育成绩大于或等于70分的学生常被成为“体育良好”，已知该校高一年级有1000名学生，试估计，高一全年级中“体育良好”的学生人数；
（Ⅱ）为分析学生平时的体育活动情况，现从体育成绩在[60，70）和[80，90）的样本学生中随机抽取2人，至少有1人体育成绩在[60，70）的概率；
（Ⅲ）假设甲、乙、丙三人的体育成绩分别为a，b，c，且分别在[70，80），[80，90），[90，100]三组中，其中a，b，c∈N，当数据a，b，c的方差s2最小时，写出a，b，c的值．（结论不要求证明）
20．已知不等式2x+4$\sqrt{xy}$≤a（x+y）对任意正数x，y都成立，求实数a的取值范围．
7．已知P={x|x2-8x-20≤0}，S={x|1-m≤x≤1+m}，是否存在实数m，使x∈P是x∈S的充要条件，若存在，求出m的范围；若不存在，请说明理由．
17．函数y=mx+1（x∈R），与y=$\frac{x}{2}$-n（n∈R）互为反函数的充要条件是m=2，n=$\frac{1}{2}$．
4．函数f（x）=tan（x-$\frac{π}{4}$）的单调区间为（　　）
A．（kπ-$\frac{π}{2}$，kπ+$\frac{π}{2}$）（k∈Z）B．（kπ，（k+1）π）（k∈Z）C．（kπ-$\frac{3π}{4}$，kπ+$\frac{π}{4}$）（k∈Z）D．（kπ-$\frac{π}{4}$，kπ+$\frac{3π}{4}$）（k∈Z）
1．已知圆的方程为x2+y2-6x=0，过点（1，2）的该圆的三条弦的长a1，a2，a3构成等差数列，则数列a1，a2，a3的公差的最大值是2．
2．设函数f（x）=emx+x2-mx（x∈R），讨论f（x）的单调性．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网