题目内容
1．已知圆的方程为x2+y2-6x=0，过点（1，2）的该圆的三条弦的长a1，a2，a3构成等差数列，则数列a1，a2，a3的公差的最大值是2．分析 化圆的一般方程为标准方程，求出圆心坐标和半径，得到最大弦长，再求出过P且垂直于CP的弦的弦长，即最小弦长，然后利用等差数列的通项公式求得公差得答案．
解答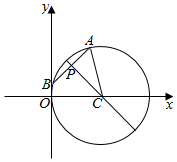 
解：如图，由x2+y2-6x=0，得（x-3）2+y2=9，
∴圆心坐标C（3，0），半径r=3，
由圆的性质可知，过点P（1，2）的该圆的弦的最大值为圆的直径，等于6，
最小值为过P且垂直于CP的弦的弦长，
∵|CP|=$\sqrt{（3-1）^{2}+（0-2）^{2}}=2\sqrt{2}$，
∴|AB|=2$\sqrt{{3}^{2}-（2\sqrt{2}）^{2}}=2$，
即a1=2，a3=6，
∴公差d的最大值为$\frac{{a}_{3}-{a}_{1}}{2}=\frac{6-2}{2}=2$．
故答案为：2．
点评 本题考查圆的性质，考查了等差数列的通项公式，是基础的计算题．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
11．已知定义在R上的函数f（x）满足f（x）=2f（x+2），当x∈[0，2）时，f（x）=x2-2x．若x∈[4，6）时，不等式f（x）≥$\frac{t}{4}$-$\frac{1}{2t}$恒成立，则t的取值范围为（ ）
| A． | [-2，0）∪[1，+∞） | B． | （-∞，2]∪（0，1] | C． | [-2，0）∪（0，1） | D． | [-2，0）∪（0，1] |
如图所示，在长方体ABCD-A1B1C1D1中，E，F分别是棱AA1和棱CC1的中点．求证：EB1∥DF，ED∥B1F．（提示：设G是DD1的中点，分别连接EG，GC1）
6．
函数f（x）=Asin（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的图象如图所示，若$\overrightarrow{PQ}$•$\overrightarrow{QS}$=$\frac{{π}^{2}}{8}$-8，则函数f（x）的解析式为（ ）
函数f（x）=Asin（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的图象如图所示，若$\overrightarrow{PQ}$•$\overrightarrow{QS}$=$\frac{{π}^{2}}{8}$-8，则函数f（x）的解析式为（ ）| A． | f（x）=2sin（3x-$\frac{π}{4}$） | B． | f（x）=2sin（3x+$\frac{π}{4}$） | C． | f（x）=2sin（2x+$\frac{π}{3}$） | D． | f（x）=2sin（2x-$\frac{π}{3}$） |
13．设lg2=a，则lg50=（ ）
| A． | 2-a | B． | 1-a | C． | 1+a | D． | 2+a |