题目内容
解分式方程：
+
-
=1的解为 ．
| 1 |
| x+2 |
| 4x |
| x2-4 |
| 2 |
| x-2 |
考点：函数的零点与方程根的关系
专题：函数的性质及应用
分析：根据分式方程的特点，进行通分即可得到结论．
解答：
解：要使方程有意义，则x≠±2，
则方程等价为
=
=
=
=1，
即x+2=3，解得x=1，
经检验得x=1成立．
故答案为：1
则方程等价为
| x-2+4x-2(x+2) |
| x2-4 |
| 3x-6 |
| x2-4 |
| 3(x-2) |
| (x-2)(x+2) |
| 3 |
| x+2 |
即x+2=3，解得x=1，
经检验得x=1成立．
故答案为：1
点评：本题主要考查分式方程的求解，比较基础．
练习册系列答案
智趣暑假温故知新系列答案
相关题目
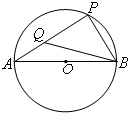如图，AB是半径为3的圆O的直径，P是圆O上异于A，B的一点Q是线段AP上靠近A的三等分点，且