题目内容
 (1)在给定的坐标系中画出函数y=2|x-1|的图象,并指出其值域和单调区间
(1)在给定的坐标系中画出函数y=2|x-1|的图象,并指出其值域和单调区间(2)函数f(x)=loga(x2-x+2),若f(x)>loga4,求x的取值范围.
考点:指、对数不等式的解法,函数图象的作法
专题:函数的性质及应用,不等式的解法及应用
分析:(1)根据指数函数的图象和性质,即可得到结论.
(2)根据对数函数的单调性,解对数不等式即可.
(2)根据对数函数的单调性,解对数不等式即可.
解答:
解:(1)∵y=2|x-1|=
,作出对应的图象如图: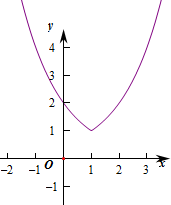
则在(-∞,1]上单调递减,在[1,+∞)上单调递增,值域是[1,+∞).
(2)当a>1时,不等式变为:x2-x+2>4,即:x2-x-2>0,解集为(-∞,-1)∪(2,+∞),
当0<a<1时,不等式变为:0<x2-x+2<4,即:x2-x-2<0,解集为(-1,2).
|

则在(-∞,1]上单调递减,在[1,+∞)上单调递增,值域是[1,+∞).
(2)当a>1时,不等式变为:x2-x+2>4,即:x2-x-2>0,解集为(-∞,-1)∪(2,+∞),
当0<a<1时,不等式变为:0<x2-x+2<4,即:x2-x-2<0,解集为(-1,2).
点评:本题主要考查指数函数的图象和性质,以及对数不等式的求解,根据函数的单调性是解决本题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目