题目内容
已知函数f(x)=ex-a(x+1),在x=ln2处的切线的斜率为1.
(1)求a的值及函数f(x)的最小值;
(2)若对于任意x∈[0,+∞)时,f(x)≥mx2恒成立,求实数m的取值范围.
(1)求a的值及函数f(x)的最小值;
(2)若对于任意x∈[0,+∞)时,f(x)≥mx2恒成立,求实数m的取值范围.
考点:利用导数研究曲线上某点切线方程,函数恒成立问题
专题:计算题,导数的综合应用
分析:(1)利用导数与切线的关系求得a,再利用导数判断函数的单调性求得最小值;
(2)令g(x)=f(x)-mx2,利用导数求得g(x)的最小值,即可得出结论.
(2)令g(x)=f(x)-mx2,利用导数求得g(x)的最小值,即可得出结论.
解答:
解:(1)∵f(x)=ex-a(x+1),
∴f′(x)=ex-a,
∵函数f(x)=ex-a(x+1)在x=ln2处的切线的斜率为1,
∴f′(ln2)=2-a=1,
∴a=1,
∴f(x)=ex-x-1,f′(x)=ex-1,
∴x<0时,f′(x)<0,x>0时,f′(x)>0,
∴x=0时,函数有极小值,即为最小值,最小值为0;
(2)令g(x)=f(x)-mx2,则g′(x)=ex-1-2mx,
设h(x)=g′(x)=ex-1-2mx,则h′(x)=ex-2m,
①m≤
时,h′(x)≥0,h(x)≥h(0)=0,∴g′(x)≥0,∴g(x)≥g(0)=0,满足题意;
②m>
时,h′(x)<0,h(x)是减函数,h(x)≤h(0)=0,∴g(x)是减函数,
∴g(ln2m)≤g(0)=0,不满足题意.
则实数m的取值范围是:(-∞,
].
∴f′(x)=ex-a,
∵函数f(x)=ex-a(x+1)在x=ln2处的切线的斜率为1,
∴f′(ln2)=2-a=1,
∴a=1,
∴f(x)=ex-x-1,f′(x)=ex-1,
∴x<0时,f′(x)<0,x>0时,f′(x)>0,
∴x=0时,函数有极小值,即为最小值,最小值为0;
(2)令g(x)=f(x)-mx2,则g′(x)=ex-1-2mx,
设h(x)=g′(x)=ex-1-2mx,则h′(x)=ex-2m,
①m≤
| 1 |
| 2 |
②m>
| 1 |
| 2 |
∴g(ln2m)≤g(0)=0,不满足题意.
则实数m的取值范围是:(-∞,
| 1 |
| 2 |
点评:本题主要考查利用导数研究函数的切线问题、研究函数的单调性最值等知识,考查学生的计算能力,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
若a=20.5,b=log20.5,c=log21.5,则( )
| A、a>b>c |
| B、a>c>b |
| C、c>a>b |
| D、b>c>a |
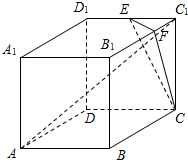 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,∠DAB=45°,AA1=AB=2,AD=2
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,∠DAB=45°,AA1=AB=2,AD=2 (1)在给定的坐标系中画出函数y=2|x-1|的图象,并指出其值域和单调区间
(1)在给定的坐标系中画出函数y=2|x-1|的图象,并指出其值域和单调区间 图中的三个直角三角形是一个几何体的三视图,
图中的三个直角三角形是一个几何体的三视图,