题目内容
20.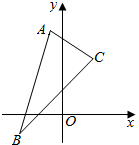 已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).
已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).(1)求BC边中线AD所在直线方程;
(2)求AC边上的垂直平分线的直线方程
(3)求点A到BC边的距离.
分析 利用直线的两点式方程、点斜式方程、直线 的斜率公式和点到直线的距离公式求解
解答 解:(1)∵B(-2,-1),C(2,3),
∴BC的中点D(0,1),又A(-1,4),
∴直线AD:$\frac{y-1}{4-1}=\frac{x}{-1}$,整理,得:3x+y-1=0.…(4分)
(2)∵△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3),
∴AC的中点E($\frac{1}{2}$,$\frac{7}{2}$),AC的斜率k=-$\frac{1}{3}$,
∴AC边上的垂直平分线的斜率为3,
∴所求直线方程y-$\frac{7}{2}$=3(x-$\frac{1}{2}$),整理,得:3x-y+2=0 …(8分)
(3)∵B(-2,-1),C(2,3),
∴直线BC:$\frac{y+1}{3+1}=\frac{x+2}{2+2}$,整理,得:x-y+1=0,
∴BC边上的高的长即点A(-1,4)到直线BC的距离,其值为d=$\frac{|-1-4+1|}{\sqrt{{1}^{2}+(-1)^{2}}}$=2$\sqrt{2}$.
点评 本题考查直线方程的求法,考查线段长的求法,是基础题,解题时要认真审题,注意点到直线的距离公式的合理运用

练习册系列答案
相关题目
10.${∫}_{0}^{1}$(2x+6x2)dx=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8.若一个底面是正三角形的三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为( ) 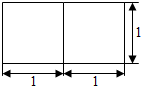

| A. | $\frac{16}{3}$ π | B. | $\frac{19}{3}$ π | C. | $\frac{19}{12}$ π | D. | $\frac{4}{3}$ π |
5.函数$f(x)=\frac{1}{x}ln(\sqrt{6-x-{x^2}}+\sqrt{{x^2}-2x})$的定义域为( )
| A. | [-3,0] | B. | [-3,0) | C. | [-3,0)∪{2} | D. | [-3,0]∪{2} |
10.某几何体的三视图如图所示,则它的表面积为( )
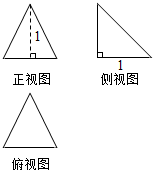

| A. | $\frac{{\sqrt{3}+\sqrt{7}+4}}{4}$ | B. | $\frac{{\sqrt{6}+2}}{2}$ | C. | $\frac{{\sqrt{2}+\sqrt{7}+1}}{2}$ | D. | $\frac{{\sqrt{2}+\sqrt{5}+1}}{2}$ |