题目内容
15.设f(x)=x2-ax+2.当x∈[1,+∞)时,f(x)≥0恒成立,求实数a的取值范围.分析 根据不等式的关系利用参数分类法,结合基本不等式的性质进行求解即可.
解答 解:由f(x)≥0得f(x)=x2-ax+2≥0,
即ax≤2+x2,
∵x∈[1,+∞),
∴a≤$\frac{2+{x}^{2}}{x}$=x+$\frac{2}{x}$,
∵x+$\frac{2}{x}$$≥2\sqrt{x•\frac{2}{x}}=2\sqrt{2}$,
当x=$\frac{2}{x}$,即x=$\sqrt{2}$取等号,
∴$a≤2\sqrt{2}$.
点评 本题主要考查不等式恒成立,利用参数分离法结合不等式是解决本题的关键.

练习册系列答案
相关题目
10.条件p:|x+1|>1,条件$q:\frac{1}{3-x}>1$,则¬q是¬p的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
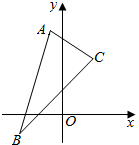 已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).
已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).