Question

16．求下列双曲线的实轴长、虚轴长、焦点坐标、顶点坐标、离心率与渐近线方程，并画出图形：
（1）x²-8y²=32；   
（2）$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1．

Answer 1

分析 双曲线转化为标准形式，得到a，b，c的值，即可得到实轴长和虚轴长、焦点坐标和顶点坐标、离心率、渐近线方程．

解答 解：（1）方程可化为$\frac{{x}^{2}}{32}-\frac{{y}^{2}}{4}=1$，∴a=4$\sqrt{2}$，b=2，c=6，
∴实轴长为8$\sqrt{2}$、虚轴长为4、焦点坐标（±6，0）、顶点坐标（$±4\sqrt{2}$，0）、离心率e=$\frac{c}{a}$=$\frac{3\sqrt{2}}{4}$，渐近线方程y=±$\frac{\sqrt{2}}{4}$x；图形如图所示．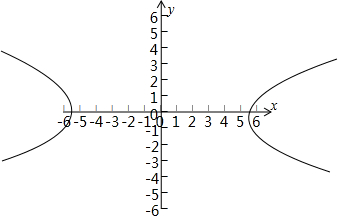

（2）a=3，b=4，c=5，
∴实轴长为6、虚轴长为8、焦点坐标（0，±5）、顶点坐标（0，3）、离心率e=$\frac{c}{a}$=$\frac{5}{3}$，渐近线方程y=±$\frac{4}{3}$x；图形如图所示．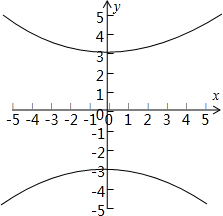

点评 本题主要考查双曲线的基本性质，要注意转化成双曲线的标准方程，再作答，考查基础知识的简单应用．