题目内容
19.已知抛物线E:x2=2py(p>0),其焦点为F,过F且斜率为1的直线被抛物线截得的弦长为8.(1)求抛物线E的方程;
(2)设A为E上一动点(异于原点),E在点A处的切线交x轴于点P,原点O关于直线PF的对称点为点B,直线AB与y轴交于点C,求△OBC面积的最大值.
分析 (1)过点F且斜率为1的直线代入抛物线,利用|MN|=8,可得y1+y2+p=8,即可求抛物线C的方程;
(2)求出直线AB的方程是y=$\frac{{t}^{2}-4}{4t}$x+1,C(0,1),可得S△OBC=|$\frac{2t}{{t}^{2}+4}$|≤$\frac{1}{2}$,即可求△OBC面积的最大值.
解答 解:(1)由题可知F(0,$\frac{p}{2}$),则该直线方程为:y=x+$\frac{p}{2}$,
代入x2=2py(p>0)得:x2-2px-p2=0,
设M(x1,y1),N(x2,y2),则有x1+x2=2p,
∵|MN|=8,∴y1+y2+p=8,即3p+p=8,解得p=2
∴抛物线的方程为:x2=4y;
(2)设A(t,$\frac{{t}^{2}}{4}$),则E在点A处的切线方程为y=$\frac{t}{2}$x-$\frac{{t}^{2}}{4}$,P($\frac{t}{2}$,0),B($\frac{4t}{{t}^{2}+4}$,$\frac{2{t}^{2}}{{t}^{2}+4}$),
直线AB的方程是y=$\frac{{t}^{2}-4}{4t}$x+1,∴C(0,1)
S△OBC=|$\frac{2t}{{t}^{2}+4}$|≤$\frac{1}{2}$,当且仅当t=±2时,取得等号,
所以△OBC面积的最大值为$\frac{1}{2}$.
点评 本题考查抛物线方程,直线与抛物线的位置关系,考查抛物线的定义,韦达定理的运用,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
9.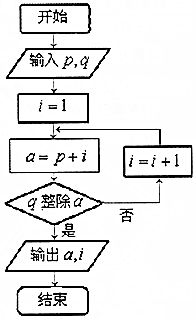 阅读如图所示的程序框图,若输入p=2,q=9,则输出的a、i的值分别为( )
阅读如图所示的程序框图,若输入p=2,q=9,则输出的a、i的值分别为( )
 阅读如图所示的程序框图,若输入p=2,q=9,则输出的a、i的值分别为( )
阅读如图所示的程序框图,若输入p=2,q=9,则输出的a、i的值分别为( )| A. | a=3,i=1 | B. | a=18,i=16 | C. | a=18,i=15 | D. | a=9,i=7 |
7.设p:x2-x<1,$q:{log_2}({x^2}-x)<0$,则非p是非q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.设△AnBnCn的三边长分别为an,bn,cn,n=1,2,3,…,若b1>c1,b1+c1=2a1,an+1=an,${b_{n+1}}=\frac{{{a_n}+{c_n}}}{2}$,${c_{n+1}}=\frac{{{a_n}+{b_n}}}{2}$,则∠An的最大值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
4.已知复数z=$\frac{(-1+i)(2+i)}{-i}$,则z在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |