题目内容
3.已知某几何体的三视图如图所示,则该几何的体积为$\frac{80}{3}$.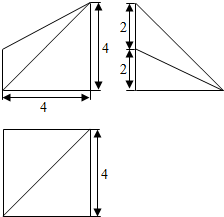
分析 以正方体为载体,根据三视图作出几何体的直观图,使用作差法求出几何体的体积.
解答 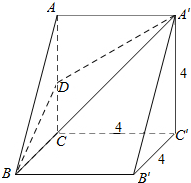 解:由三视图可知几何体为直三棱柱ABC-A'B'C'中切去三棱锥B-ADA'得到的.
解:由三视图可知几何体为直三棱柱ABC-A'B'C'中切去三棱锥B-ADA'得到的.
其中,直三棱柱的底面ABC是等腰直角三角形,直角边为4,棱柱的高为4,D为AC的中点.
直三棱柱ABC-A'B'C'的体积为$\frac{1}{2}×4×4×4$=32.
三棱锥B-ADA'的体积为$\frac{1}{3}×\frac{1}{2}×4×2×4$=$\frac{16}{3}$.
∴几何体的体积V=32-$\frac{16}{3}$=$\frac{80}{3}$.
故答案为:$\frac{80}{3}$.
点评 本题考查了不规则几何体的三视图和体积计算,属于中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
8.已知向量$\overrightarrow{a}$=(1,2,1),$\overrightarrow{b}$=(x,-1,1),若$\overrightarrow{a}⊥\overrightarrow{b}$,则实数x的值为( )
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
12.等比数列{an}中,a1、a8是方程x2+2x-5=0的两个根,则a4a5等于( )
| A. | -5 | B. | -2 | C. | 2 | D. | 5 |

 如图所示,已知正方体ABCD-A1B1C1D1中,G,H分别是的B1C1,C1D1中点,求证:DH,BG,CC1延长后相交于一点.
如图所示,已知正方体ABCD-A1B1C1D1中,G,H分别是的B1C1,C1D1中点,求证:DH,BG,CC1延长后相交于一点.