题目内容
14.已知函数f(x)=|2x-3|,g(x)=x-1.(1)求不等式f(x)≤|g(x)|的解集;
(2)求不等式f(x)≤g(x)的解集.
分析 (1)问题转化为|2x-3|≤|x-1|,两边平方,求出不等式的解集即可;(2)f(x)≤g(x),即|2x-3|≤x-1,显然x-1≥0,解法同(1).
解答 解:函数f(x)=|2x-3|,g(x)=x-1.
(1)不等式f(x)≤|g(x)|,
即|2x-3|≤|x-1|,
∴(2x-3)2≤(x-1)2,
解得:$\frac{4}{3}$≤x≤2,
故不等式的解集是[$\frac{4}{3}$,2];
(2)不等式f(x)≤g(x),
即|2x-3|≤x-1,显然x-1≥0,
x-1≥0,即x≥1时,
由(1)得:$\frac{4}{3}$≤x≤2,
故不等式的解集是[$\frac{4}{3}$,2].
点评 本题考查了解绝对值不等式问题,考查分类讨论,是一道中档题

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
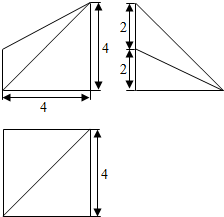
4.一个几何体的三视图如所示,则该几何体的体积是( )


| A. | $\frac{2}{3}$π+4 | B. | 2π+4 | C. | π+4 | D. | π+2 |
5.若集合A=[2,3],B={x|x2-5x+6=0|,则A∩B=( )
| A. | {2,3} | B. | ∅ | C. | 2 | D. | [2,3] |
9.奇函数f(x)的定义域为R,若f(x+1)为偶函数,且f(1)=2,则f(4)+f(5)的值为( )
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=∠DAB=90°,SA⊥平面ABCD,SA=AB=BC=2,AD=1,M为SB的中点,过点M、A、D的截面MADN交SC于点N.
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=∠DAB=90°,SA⊥平面ABCD,SA=AB=BC=2,AD=1,M为SB的中点,过点M、A、D的截面MADN交SC于点N.