题目内容
6.已知抛物线C:y2=2px(p>0)过点A(1,m),B为抛物线的准线与x轴的交点,若|AB|=2$\sqrt{2}$.(1)求抛物线的方程;
(2)在抛物线上任取一点P(x0,2),过点P作两条直线分别与抛物线另外相交于点M,N,连接MN,若直线
PM,PN,MN的斜率都存在且不为零,设其斜率分别为k1,k2,k3,求$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$-$\frac{1}{{k}_{3}}$的值.
分析 (1)抛物线C:y2=2px(p>0)过点A(1,m),可得m2=2p,由B为抛物线的准线与x轴的交点,可得B$(-\frac{p}{2},0)$.根据|AB|=2$\sqrt{2}$,即可得出.
(2)在抛物线上任取一点P(x0,2),4x0=22,解得P(1,2).设M(x1,y1),N(x2,y2),直线PM的方程为:y-2=k1(x-1),与抛物线方程联立化为:${y}^{2}-\frac{4}{{k}_{1}}$y+$\frac{8}{{k}_{1}}$-4=0,解得M$(\frac{(2-{k}_{1})^{2}}{{k}_{1}^{2}},\frac{4}{{k}_{1}}-2)$.同理可得:N$(\frac{(2-{k}_{2})^{2}}{{k}_{2}^{2}},\frac{4}{{k}_{2}}-2)$.再利用斜率计算公式化简即可得出.
解答 解:(1)∵抛物线C:y2=2px(p>0)过点A(1,m),
∴m2=2p,
∵B为抛物线的准线与x轴的交点,∴B$(-\frac{p}{2},0)$.
又|AB|=2$\sqrt{2}$,
∴(1+$\frac{p}{2}$)2+m2=8,
∵p>0,∴p=2,
∴抛物线的方程为y2=4x.
(2)在抛物线上任取一点P(x0,2),∴4x0=22,解得x0=1,∴P(1,2).
设M(x1,y1),N(x2,y2),直线PM的方程为:y-2=k1(x-1),
联立$\left\{\begin{array}{l}{y-2={k}_{1}(x-1)}\\{{y}^{2}=4x}\end{array}\right.$,化为:${y}^{2}-\frac{4}{{k}_{1}}$y+$\frac{8}{{k}_{1}}$-4=0,
解得y=2或y=$\frac{4}{{k}_{1}}-2$.∴x1=$\frac{{y}_{1}^{2}}{4}$=$\frac{(2-{k}_{1})^{2}}{{k}_{1}^{2}}$,∴M$(\frac{(2-{k}_{1})^{2}}{{k}_{1}^{2}},\frac{4}{{k}_{1}}-2)$.
同理可得:N$(\frac{(2-{k}_{2})^{2}}{{k}_{2}^{2}},\frac{4}{{k}_{2}}-2)$.
∴k3=$\frac{\frac{4}{{k}_{2}}-2-(\frac{4}{{k}_{1}}-2)}{\frac{(2-{k}_{2})^{2}}{{k}_{2}^{2}}-\frac{(2-{k}_{1})^{2}}{{k}_{1}^{2}}}$=$\frac{{k}_{1}{k}_{2}}{({k}_{1}+{k}_{2})-{k}_{1}{k}_{2}}$,
可得$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$-$\frac{1}{{k}_{3}}$=1.
点评 本题考查了抛物线的标准方程及其性质、直线与抛物线相交问题、一元二次方程的根与系数的关系、斜率计算公式,考查了推理能力与计算能力,属于难题.

| A. | 3 | B. | $\frac{57}{7}$ | C. | 28 | D. | 31 |
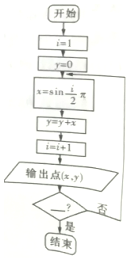
| A. | i>8 | B. | i>7 | C. | i>6 | D. | i>5 |
| A. | $({-∞,-\frac{1}{4}}]$ | B. | $[{-\frac{1}{4},+∞})$ | C. | $({-∞,-\frac{3}{4}}]$ | D. | $[{-\frac{3}{4},+∞})$ |
| A. | ∅ | B. | {0} | C. | [0,1] | D. | {0,1} |
| A. | c<a<b | B. | a<b<c | C. | b<c<a | D. | b<a<c |