题目内容
5.已知函数f(x)=$\sqrt{3}$sinxcosx-$\frac{1}{2}$cos2x.(1)求函数f(x)的最小正周期;
(2)在△ABC中,角A,B,C的对边分别为a,b,c,若a=$\sqrt{2}$,b=1,f($\frac{A}{2}$+$\frac{π}{3}$)=$\frac{1}{3}$,求sinB的值.
分析 (1)由条件利用两角和差的三角公式,化简函数的解析式,再根据正弦函数的周期性求得f(x)的最小正周期.
(2)由f($\frac{A}{2}$+$\frac{π}{3}$)=$\frac{1}{3}$,求得cosA的值,可得sinA的值,再利用正弦定理求得sinB的值.
解答 解:(1)函数f(x)=$\sqrt{3}$sinxcosx-$\frac{1}{2}$cos2x=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$cos2x=sin(2x-$\frac{π}{6}$),
故f(x)的最小正周期为T=$\frac{2π}{2}$=π.
(2)由f($\frac{A}{2}$+$\frac{π}{3}$)=$\frac{1}{3}$,得sin(A+$\frac{π}{2}$)=$\frac{1}{3}$,则 cosA=$\frac{1}{3}$,
在△ABC中,sinA=$\sqrt{{1-cos}^{2}A}$=$\frac{2\sqrt{2}}{3}$.
又因为a=$\sqrt{2}$,b=1,由正弦定理可得sinB=$\frac{b}{a}$sinA=$\frac{2}{3}$.
点评 本题主要考查两角和差的三角公式,正弦函数的周期性,同角三角函数的基本关系,正弦定理的应用,属于中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
13.函数f(x)=2x3+5$\sqrt{2{x^3}-1}$的最小值是( )
| A. | -3? | B. | 1 | C. | $-\frac{21}{4}$? | D. | 7 |
10.下面几种推理过程是演绎推理的是( )
| A. | 两条直线平行,同旁内角互补,如果∠A和∠B是两条平行直线的同旁内角,则∠A+∠B=180° | |
| B. | 由平面三角形的性质,推测空间四面体的性质 | |
| C. | 某校高三共有10个班,1班有51人,2班有53人,三班有52人,由此推测各班都超过50人 | |
| D. | 在数列{an}中,a1=1,an=$\frac{1}{2}$(an-1+$\frac{1}{{a}_{n-1}}$)(n≥2),计算a2、a3,a4,由此猜测通项an |
17.若x,y满足约束条件$\left\{\begin{array}{l}{x+2y-2≥0}\\{x-y+3≥0}\\{x≤3}\end{array}\right.$,则z=2x+y的最大值为12.
15.设f:A→B是从集合A到集合B的映射,则下列说法正确的是( )
| A. | A中不同元素的像必不同 | |
| B. | A中每一个元素在B中必有像 | |
| C. | B中每一个元素在A中必有原像 | |
| D. | B中每一个元素在A中必有唯一的原像 |
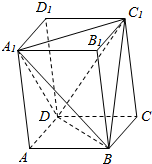 已知四棱锥ABCD-A1B1C1D1的底面是边长为2的正方形,侧棱AA1⊥底面ABCD,若得二面角A1-BD-C1的大小为60°,求四棱柱ABCD-A1B1C1D1的体积.
已知四棱锥ABCD-A1B1C1D1的底面是边长为2的正方形,侧棱AA1⊥底面ABCD,若得二面角A1-BD-C1的大小为60°,求四棱柱ABCD-A1B1C1D1的体积.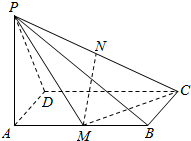 如图,已知PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点,若AD=PA=a,AB=$\sqrt{2}$a.
如图,已知PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点,若AD=PA=a,AB=$\sqrt{2}$a.