题目内容
17.若x,y满足约束条件$\left\{\begin{array}{l}{x+2y-2≥0}\\{x-y+3≥0}\\{x≤3}\end{array}\right.$,则z=2x+y的最大值为12.分析 作出不等式组对应的平面区域,利用目标函数的几何意义,求最大值.
解答 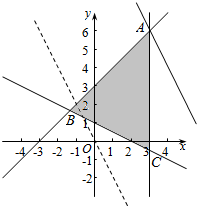 解:作出不等式组对应的平面区域如图:(阴影部分).
解:作出不等式组对应的平面区域如图:(阴影部分).
由z=2x+y得y=-2x+z,
平移直线y=-2x+z,
由图象可知当直线y=-2x+z经过点A时,直线y=-2x+z的截距最大,
此时z最大.
由$\left\{\begin{array}{l}{x=3}\\{x-y+3=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=3}\\{y=6}\end{array}\right.$,即A(3,6),
代入目标函数z=2x+y得z=2×3+6=6+6=12.
即目标函数z=2x+y的最大值为12.
故答案为:12.
点评 本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
7.设F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两个焦点,点A是以F1为圆心,b为半径的圆与双曲线的一个交点,且AF2与圆相切,则该双曲线的离心率为( )
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{5}$ | D. | $\sqrt{5}$ |
8.已知定义在R上的函数f(x)满足①f(2-x)=f(x);②f(x+2)=f(x-2);③x1,x2∈[1,3]时,$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0,则f(2014),f(2015),f(2016)大小关系为( )
| A. | f(2014)>f(2015)>f(2016) | B. | f(2016)>f(2014)>f(2015) | ||
| C. | f(2016)=f(2014)>f(2015) | D. | f(2014)>f(2015)=f(2016) |
12.已知双曲线的渐近线方程为y=±$\frac{1}{2}$x,且经过点(4,1),则双曲线的标准方程为( )
| A. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{12}$=1 | B. | $\frac{{y}^{2}}{3}$-$\frac{{x}^{2}}{12}$=1 | C. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{y}^{2}}{12}$-$\frac{{x}^{2}}{3}$=1 |
2.已知函数f(x)=lnx+2的图象与直线y=x+a恰好有一个交点,设g(x)=ex-$\frac{1}{2}$x2-ax,当x∈[1,2]时,不等式-m≤g(x)≤m2-4恒成立,则实数m的取值范围是( )
| A. | (-∞,-e+$\frac{3}{2}$] | B. | [-e+$\frac{3}{2}$,e] | C. | [-e,e] | D. | [e,+∞) |
7.直线x+2y+3=0上的点P在x-y=1的上方,且P到直线2x+y-6=0的距离为3$\sqrt{5}$,则点P的坐标是( )
| A. | (-5,1) | B. | (-1,5) | C. | (-7,2) | D. | (2,-7) |
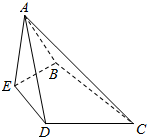 等边△ABC中,D,E分别是AC,AB的中点,沿DE将△ADE折起,使平面ADE⊥平面BCDE(如图所示).
等边△ABC中,D,E分别是AC,AB的中点,沿DE将△ADE折起,使平面ADE⊥平面BCDE(如图所示).