题目内容
10.在△ABC中,sinA,ainB,sinC成等比数列,则当cosB的值最小时,$\frac{1}{tanA}$+$\frac{1}{tanC}$=$\frac{2\sqrt{3}}{3}$.分析 根据等比数列与正弦、余弦定理,利用基本不等式求出cosB的最小值,
得出此时A=B=C=$\frac{π}{3}$,从而求出$\frac{1}{tanA}$+$\frac{1}{tanC}$的值.
解答 解:△ABC中,sinA,ainB,sinC成等比数列,
∴sin2B=sinAsinC,
∴b2=ac;
∴cosB=$\frac{{a}^{2}{+c}^{2}{-b}^{2}}{2ac}$≥$\frac{2ac-ac}{2ac}$=$\frac{1}{2}$,
当且仅当a=c时取“=”;
∴cosB的最小值是$\frac{1}{2}$,且a=c;
∴A=C,
∴A=B=C=$\frac{π}{3}$,
∴$\frac{1}{tanA}$+$\frac{1}{tanC}$=$\frac{1}{\sqrt{3}}$+$\frac{1}{\sqrt{3}}$=$\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查了正弦、余弦定理及等比数列的性质与应用问题,也考查了基本不等式的应用问题,是综合题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.从数字1,2,3,4,5中,随机抽取3个数字(允许重复)组成一个三位数,其各位数字之和等于12的概率为( )
| A. | $\frac{2}{25}$ | B. | $\frac{13}{125}$ | C. | $\frac{18}{125}$ | D. | $\frac{9}{125}$ |
20.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,O为坐标原点,M为长轴的一个端点,若在椭圆上存在点N,使ON⊥MN,则离心率e的取值范围为( )
| A. | $(\frac{{\sqrt{2}}}{2},1)$ | B. | $(0,\frac{{\sqrt{2}}}{2})$ | C. | $(\frac{{\sqrt{3}}}{2},1)$ | D. | $(0,\frac{{\sqrt{3}}}{2})$ |
 对于任意
对于任意 恒成立;
恒成立;  ,如果命题“
,如果命题“ 为真,
为真, 为假”,求实数
为假”,求实数 的取值范围.
的取值范围.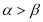 ,则
,则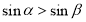 ;
;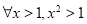 ”的否定是“
”的否定是“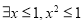 ”;
”;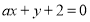 与
与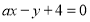 垂直的充要条件为
垂直的充要条件为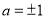 ;
; ,则
,则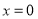 或
或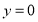 ”的逆否命题为“若
”的逆否命题为“若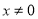 或
或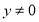 ,则
,则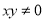 ”
”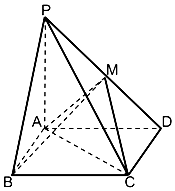 如图,在四棱锥P-ABCD,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.
如图,在四棱锥P-ABCD,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.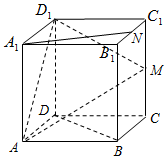 如图边长为2的正方体ABCD-A1B1C1D1中,M,N分别是CC1,B1C1的中点,
如图边长为2的正方体ABCD-A1B1C1D1中,M,N分别是CC1,B1C1的中点,